Trend - Properties - Additional

Trend: Introduction

Trend: Enhanced

Trend: Language

Local Group

Preface

Goal: Exploring additional statistic properties not related to trend.

There are also common properties for statistics not related with trend. In trend context let’s call them additional properties. This properties is important for other statistics analysis.

Before you integrate the statistic properties, into your super duper application. You’d better make a good modelling to make sure your code get the right output result. You can make mathematical model using spreadsheet, but first you should understand the math behind the formula.

Equation

We begin with equation symbol, as our base of calculation.

Min, Max, Range

It is obvious.

$\begin{align*} && \text{min} &= \min(x_1, x_2, \ldots, x_n) \\ && \text{max} &= \max(x_1, x_2, \ldots, x_n) \\ && \text{range} &= \text{max} - \text{min} \\ \end{align*}$

Where the max function can be express in set notation:

$\text{max}(x_i) = \{ x \in x_i \mid x \text{ is the largest element in } x_i \}$

Pretty explanatory

Median

The median can be described as below:

$Md_x = \begin{cases} x_{\frac{n+1}{2}} & \text{if } n \text{ is odd} \\ \frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2} & \text{if } n \text{ is even} \end{cases}$

Mode

We need two steps to find the modus. First we have to find frequencies, then find the maximum frequencies, and finally get the value of that frequencies.

To find the frequencies of each unique value in a dataset, where I() is the indicator function, which equals 1 if the condition is true and 0 otherwise.

$f_i = \sum_{j=1}^{n} I(x_j = x_i)$

Then we find the maximum frequency.

$f_{max} = \max\{f_1, f_2, \ldots, f_k\}$

Or in the set notation as:

$f_{max}={f_i∈{f_1,f_2,…,f_k}∣f_i \text{ is the largest element in } {f_1,f_2,…,f_k}}$

Mathematically, you would find the mode value using this equation:

$Mo_x = \{ x_i \mid f_i = f_{max} \}$

Or in oneliner fashioned all three above, can be rewritten as one set as follows:

$x_{mode} = \{ x_i \mid f_i = \max\{ \sum_{j=1}^{n} [x_j = x_i] \} \}$

SEM (Standard Error of the Mean)

The equation for SEM is:

$SEM = \frac{s}{\sqrt{n}}$

Kurtosis and Skewness

The equation for Kurtosis and Skewness can found by using this equation:

$\begin{align*} && \text{Kurtosis} &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})^4}{n \cdot s^4} - 3 \\ && \text{Skewness} &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})^3}{n \cdot s^3} \\ \end{align*}$

Standard Error of Kurtosis and Skewness

The Standard Error equation for both Kurtosis and Skewness can be tricky, and can be differ from one reference to another.

The simplified approximation of Standard Error can be expressed as below:

$\begin{align*} && SE_k &= \sqrt{\frac{24}{(n-1)}} \\ && SE_s &= \sqrt{\frac{6}{(n-1)}} \\ \end{align*}$

While the complex Standard Error equation can be described as follows:

$\begin{align*} && SE_k &= \sqrt{\frac{24n(n-2)(n-3)}{(n+1)(n+3)(n-1)^2}} \\ && SE_s &= \sqrt{\frac{6n(n-1)}{(n-2)(n+1)(n+3)}} \\ \end{align*}$

From stackoverflow I found out that, on different software the equation of Standard Error of gaussian kurtosis, can be expressed as follows.

$SE_k = \sqrt{\frac{4(n^2-1) \times SE_s^2}{(n-3)(n+5)}}$

I’m simply copying and pasting the code published by Howard Seltman in here:

spssSkewKurtosis.R

Note that above equation only applied for data that follow gaussian distribution.

Worksheet Formula

I have already prepare the built in formula for these statistics properties.

Worksheet Source

Playsheet Artefact

The Excel file is available, so you can have fun, modify as you want.

github.com/…/math/trend/examples-properties.xlsx

Min, Max, Range

It is also obvious.

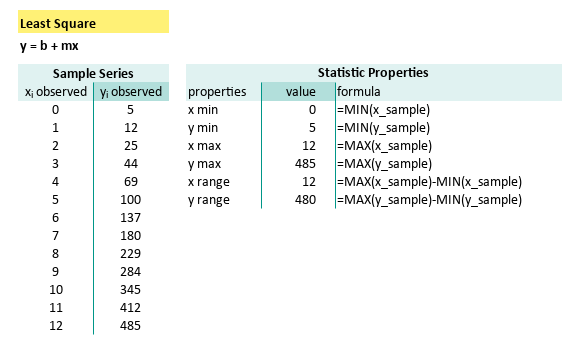
Trend: Worksheet: Min, Max, Range

These simple formulas can be summarized as follows:

properties	formula
x min	=MIN(x_sample)
y min	=MIN(y_sample)
x max	=MAX(x_sample)
y max	=MAX(y_sample)
x range	=MAX(x_sample)-MIN(x_sample)
y range	=MAX(y_sample)-MIN(y_sample)

Median and Mode

We can use built-in median() formula. But we should be careful while i uderstanding the mode() formula. For example for a completely unique data series, the result should be no mode, because all data frequency is 1. Then our beloved spreadsheet is right to give error as `#VALUE1’.

The solution is make a new helper column to calculate frequency. Let’s name the range as x_freq and y_freq, and we can use our excel/calc expertise to craft this formula:

=INDEX(y_sample, MATCH(MAX(y_freq), y_freq, 0))

The summary can be descirbed as follows:

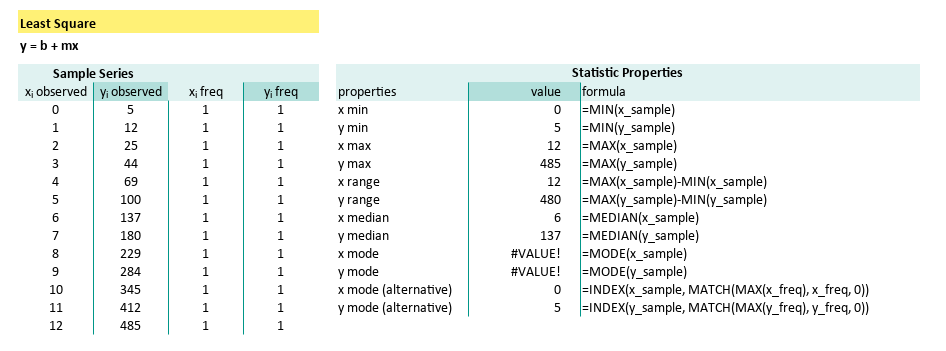
Trend: Worksheet: Median and Mode

properties	formula
x median	=MEDIAN(x_sample)
y median	=MEDIAN(y_sample)
x mode	=MODE(x_sample)
y mode	=MODE(y_sample)
x mode (alternative)	=INDEX(x_sample, MATCH(MAX(x_freq), x_freq, 0))
y mode (alternative)	=INDEX(y_sample, MATCH(MAX(y_freq), y_freq, 0))
x SE Mean	=STDEV.S(x_sample) / SQRT(COUNT(x_sample))
y SE Mean	=STDEV.S(y_sample) / SQRT(COUNT(y_sample))

Kurtosis and Skewness

Excel/Calc has built in formula KURT() and SKEW(). But unfortunately no built-in formula for standard error. With equation above, we can craft our SE formula as follows:

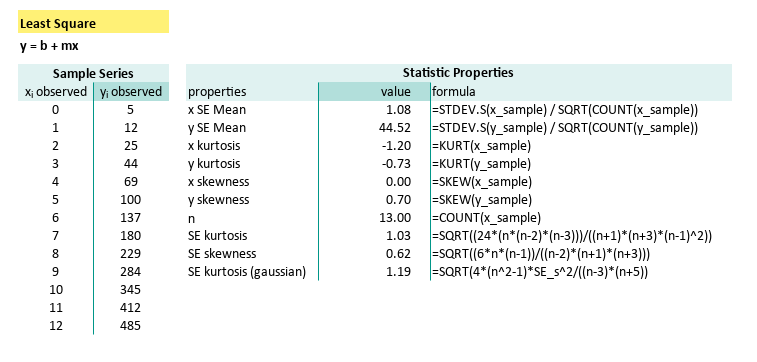
Trend: Worksheet: Kurtosis and Skewness

properties	formula
x kurtosis	=KURT(x_sample)
y kurtosis	=KURT(y_sample)
x skewness	=SKEW(x_sample)
y skewness	=SKEW(y_sample)
n	=COUNT(x_sample)
SE kurtosis	=SQRT((24(n(n-2)(n-3)))/((n+1)(n+3)*(n-1)^2))
SE skewness	=SQRT((6n(n-1))/((n-2)(n+1)(n+3)))
SE kurtosis (gaussian)	=SQRT(4(n^2-1)SE_s^2/((n-3)*(n+5))

It is fun to play with these two properties, if you understand the concept. We will also give you the visualization in this article.

Outliers

Actually, this one is interesting. But we are going to postpone.

Maybe in another article someday.

Python Tools

We can calculate additional statistic properties with python.

Python Source

The source can be obtained here:

github.com/…/trend/61-additional.py

Data Source

Instead of hardcoded data, we can setup the source data in CSV.

github.com/…/trend/50-samples.csv:

Min, Max, Range

Using the examples above:

import numpy as np

# Getting Matrix Values
pairCSV = np.genfromtxt("50-samples.csv",
  skip_header=1, delimiter=",", dtype=int)

# Extract x and y values from CSV data
x_observed = pairCSV[:, 0]
y_observed = pairCSV[:, 1]

# Number of data points
n = len(x_observed)

Python: Additional Statistical Properties: Data Series

We can calculate

# Calculate maximum, minimum, and range
x_max = np.max(x_observed)
x_min = np.min(x_observed)
x_range = x_max - x_min

y_max = np.max(y_observed)
y_min = np.min(y_observed)
y_range = y_max - y_min

# Output of maximum, minimum, and range
print('x (max, min, range) = '
 + f'({x_min:7.2f}, {x_max:7.2f}, {x_range:7.2f} )')
print('y (max, min, range) = '
 + f'({y_min:7.2f}, {y_max:7.2f}, {y_range:7.2f} )')
print()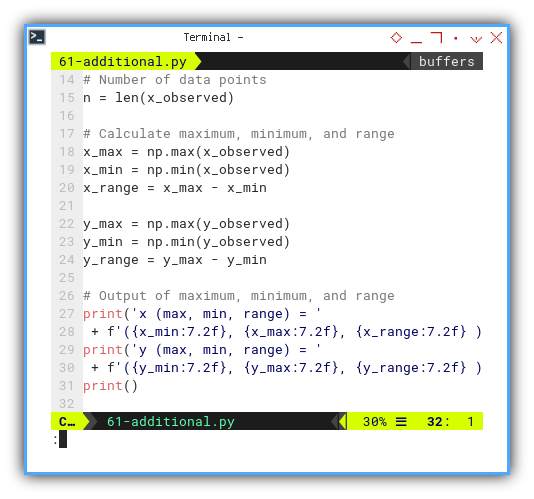

Python: Additional Statistical Properties: Min, Max, Range

Median and Mode

We can find mode using statistics library.

import statistics

x_mode = statistics.mode(x_observed)
y_mode = statistics.mode(y_observed)

We can implement above equation to find median:

def calc_median(data: np.array) -> float:
  # Sort the data
  sorted_data = np.sort(data)

  # Calculate the median
  n = len(sorted_data)
  if n % 2 == 1:
    # If odd number of data points
    median = sorted_data[n // 2]
  else:
    # If even number of data points
    median = (sorted_data[n // 2 - 1] \
           +  sorted_data[n // 2]) / 2
  
  return median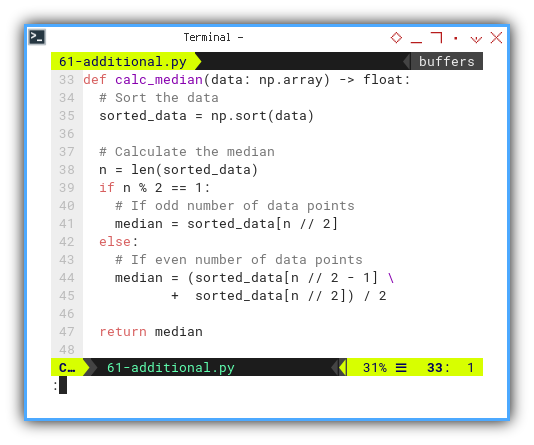

Python: Additional Statistical Properties: Median Calculation

And display.

# Calculate additional propeties
x_median = calc_median(x_observed)
y_median = calc_median(y_observed)

x_mode = statistics.mode(x_observed)
y_mode = statistics.mode(y_observed)

# Output of additional propeties
print(f'x median       = {x_median:9.2f}')
print(f'y median       = {y_median:9.2f}')
print(f'x mode         = {x_mode:9.2f}')
print(f'y mode         = {y_mode:9.2f}')
print()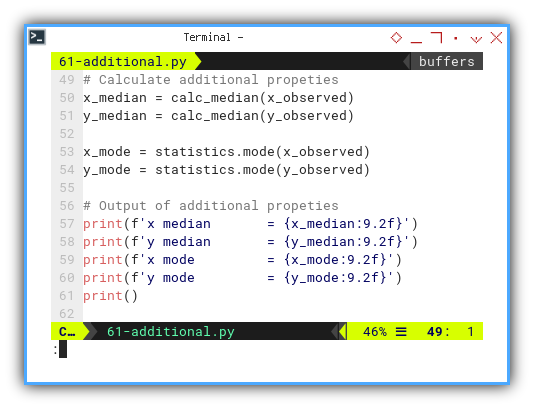

Python: Additional Statistical Properties: Median and Mode

You can also utilize

y_mode = np.argmax(np.bincount(y_observed))

Kurtosis and Skewness

We can use scipy.stat to calculate kurtosis and skewness.

from scipy.stats import kurtosis, skew

# Calculate kurtosis and skewness
x_kurtosis = kurtosis(x_observed, bias=False)
y_kurtosis = kurtosis(y_observed, bias=False)

x_skewness = skew(x_observed, bias=False)
y_skewness = skew(y_observed, bias=False)

print(f'x kurtosis     = {x_kurtosis:9.2f}')
print(f'y kurtosis     = {y_kurtosis:9.2f}')
print(f'x skewness     = {x_skewness:9.2f}')
print(f'y skewness     = {y_skewness:9.2f}')
print()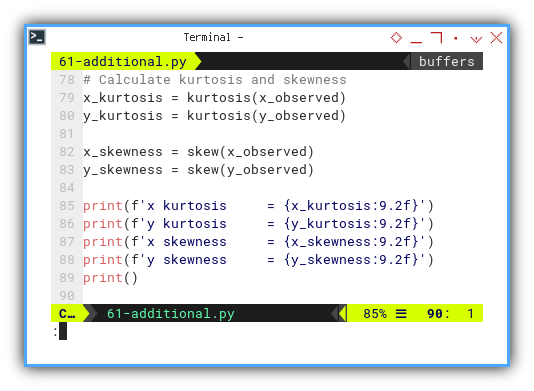

Python: Additional Statistical Properties: Kurtosis and Skewness

Standard Error of Kurtosis and Skewness

We should craft our own method to get the standard errors.

def calc_se_kurtosis(n):
  return np.sqrt( \
    (24 * n * (n - 2) * (n - 3)) \
    / ((n + 1) * (n + 3) * (n - 1) ** 2))

def calc_se_skewness(n):
  return np.sqrt( \
    (6 * n * (n - 1)) \
    / ((n - 2) * (n + 1) * (n + 3)))

def calc_se_kurtosis_gaussian(n):
  return np.sqrt( \
    (4 * n**2 * calc_se_skewness(n)**2) \
    / ((n - 3) * (n + 5)))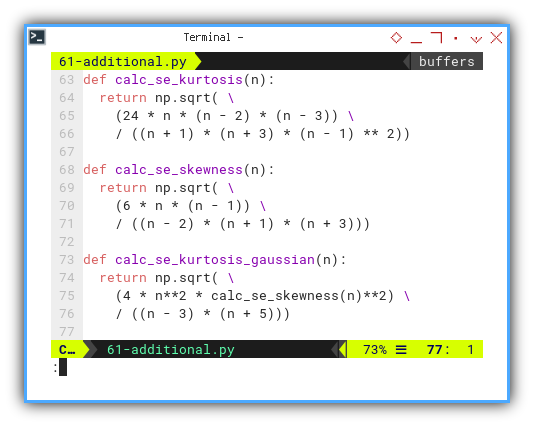

Python: Additional Statistical Properties: Standard Error Calculation

Then we can display as usual:

# number of data points
x_n = len(x_observed)
y_n = len(y_observed)

# Calculate SE kurtosis and SE skewness
x_se_kurtosis = calc_se_kurtosis_gaussian(x_n)
y_se_kurtosis = calc_se_kurtosis_gaussian(y_n)
x_se_skewness = calc_se_skewness(x_n)
y_se_skewness = calc_se_skewness(y_n)

print(f'x SE kurtosis  = {x_se_kurtosis:9.2f}')
print(f'y SE kurtosis  = {y_se_kurtosis:9.2f}')
print(f'x SE skewness  = {x_se_skewness:9.2f}')
print(f'y SE skewness  = {y_se_skewness:9.2f}')
print()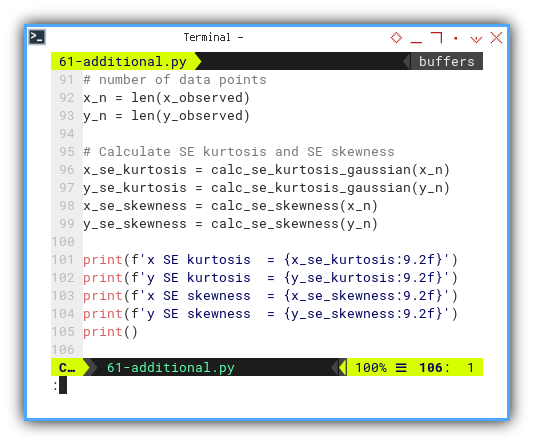

Python: Additional Statistical Properties: Standard Error

Output Result

x (max, min, range) = (   0.00,   12.00,   12.00 )
y (max, min, range) = (   5.00,  485.00,  480.00 )

x median       =      6.00
y median       =    137.00
x mode         =      0.00
y mode         =      5.00

x kurtosis     =     -1.20
y kurtosis     =     -0.73
x skewness     =      0.00
y skewness     =      0.70

x SE kurtosis  =      1.19
y SE kurtosis  =      1.19
x SE skewness  =      0.62
y SE skewness  =      0.62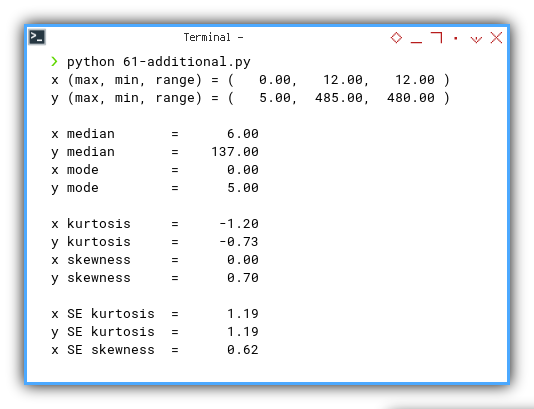

Python: Additional Statistical Properties: Output Result

Interactive JupyterLab

You can obtain the interactive JupyterLab in this following link:

github.com/…/trend/61-additional.ipynb

Properties Visualization

Now it is a good time to get the interpretation, of above additional statistic properties, in visualization using python matplotlib.

Min, Max, Range, Median and Mode

Using scatter plot we can put the statistic properties in horizontal line.

github.com/…/trend/62-plot.py

# Add horizontal lines for properties
plt.axhline(y_median, c='r', ls='--',
  label=f'Median: {y_median}')
plt.axhline(y_mean,   c='g', ls='--',
  label=f'Mean: {y_mean:.2f}')
plt.axhline(y_mode,   c='m', ls='--',
  label=f'Mode: {y_mode}')
plt.axhline(y_min,    c='c', ls='--',
  label=f'Min: {y_min}')
plt.axhline(y_max,    c='y', ls='--',
  label=f'Max: {y_max}')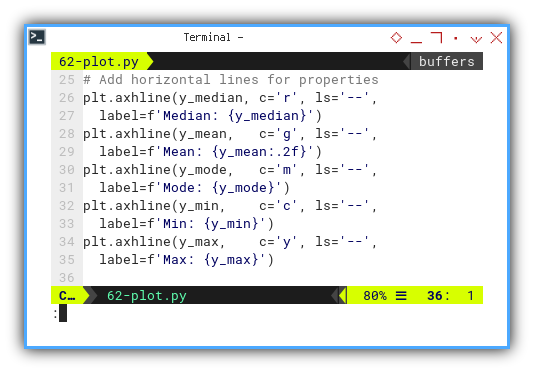

Python: Visualization: Statistic Properties: Horizontal Line

The result of the plot can be visualized as below:

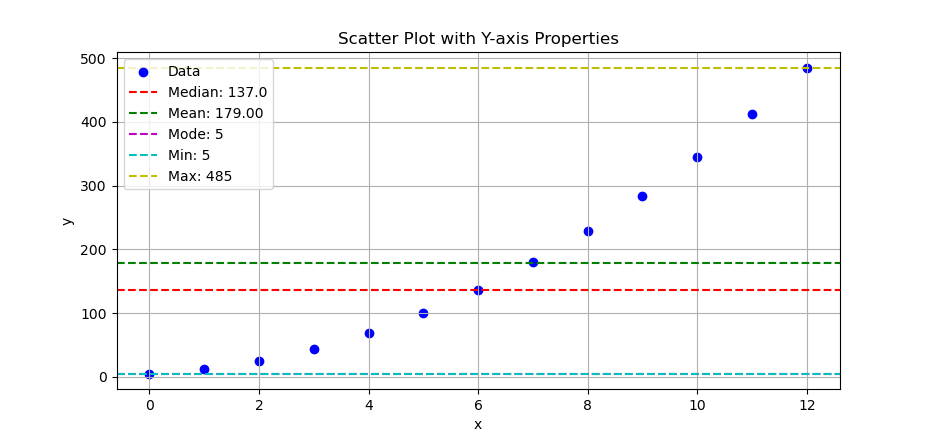
Python: Plot: Statistic Properties: Horizontal Line

You can obtain the interactive JupyterLab in this following link:

github.com/…/trend/62-plot.ipynb

Histogram and Distribution Curve

You can create a histogram, and overlay a normal distribution curve on top of it.

github.com/…/trend/66-plot-normal.py

# Calculate skewness and kurtosis of y
y_skewness = np.mean(
  ((y_observed - y_mean) / y_std) ** 3)
y_kurtosis = np.mean(
  ((y_observed - y_mean) / y_std) ** 4)

# Create histogram
plt.hist(y_observed, bins=10,
  density=True, alpha=0.6, color='cyan')

# Create range for x values
x_range = np.linspace(
  min(y_observed), max(y_observed), 100)

y_dist = norm.pdf(x_range, y_mean, y_std)

# Plot normal distribution curve
plt.plot(x_range, y_dist, color='blue',
  label='Normal Distribution')

Python: Visualization: Statistic Properties: Histogram

The result of the plot can be visualized as below:

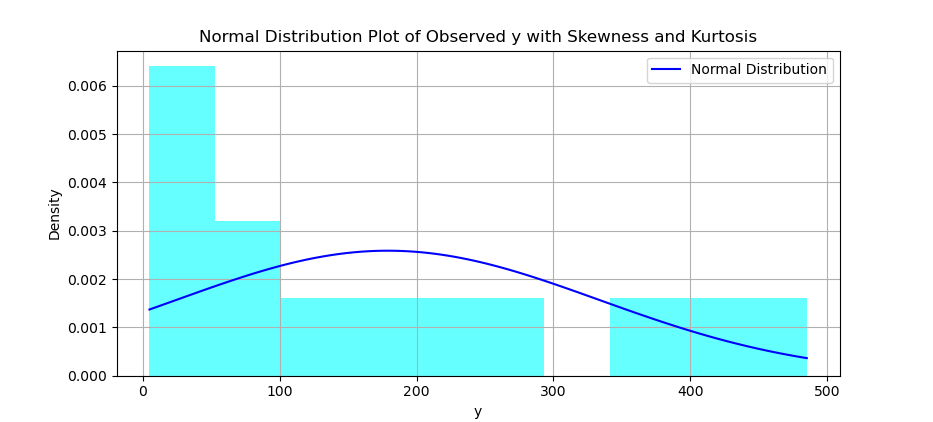
Python: Distribution Curve Plot: Histogram and Distribution Curve

You can obtain the interactive JupyterLab in this following link:

github.com/…/trend/66-plot-normal.ipynb

Revisited: Min, Max, Range, Median and Mode

Using scatter plot we can put the statistic properties, but this time in vertical line.

github.com/…/trend/68-plot-props.py

# Add vertical lines for properties
plt.axvline(y_median, c='r', ls='--',
  label=f'Median: {y_median}')
plt.axvline(y_mean,   c='g', ls='--',
  label=f'Mean: {y_mean:.2f}')
plt.axvline(y_mode,   c='m', ls='--',
  label=f'Mode: {y_mode}')
plt.axvline(y_min,    c='c', ls='--',
  label=f'Min: {y_min}')
plt.axvline(y_max,    c='y', ls='--',
  label=f'Max: {y_max}')

Python: Visualization: Statistic Properties: Vertical Line

The result of the plot can be visualized as below:

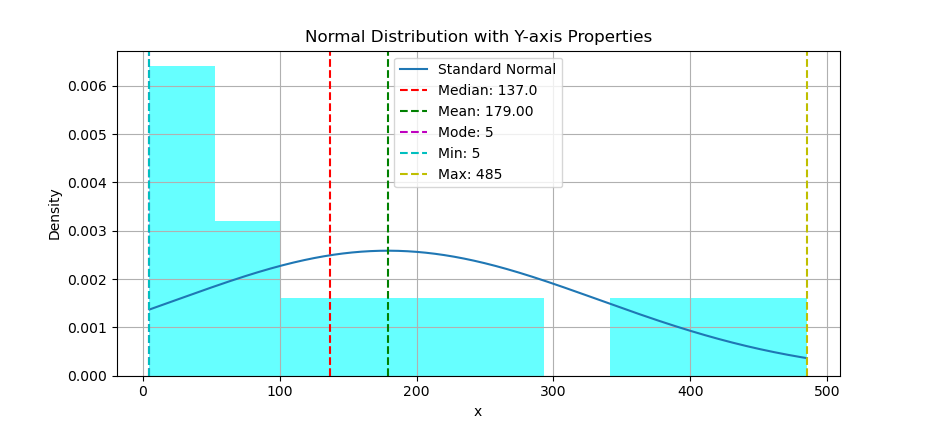
Python: Distribution Curve Plot: Statistic Properties: Vertical Line

You can obtain the interactive JupyterLab in this following link:

github.com/…/trend/67-plot-ks.ipynb

Kurtosis and Skewness

With histogram, you can also overlay a distribution curve, with applied kurtosis and skewness.

github.com/…/trend/67-plot-ks.py

First we need to calculate the corresponding y-values for the standard normal distribution. Then we need to adjust the shape parameter manually to achieve the desired kurtosis You may need to experiment with different values to get closer to the desired kurtosis. Then calculate the corresponding y-values for skewnorm distribution with given skewness and adjusted shape parameter. Finally plot both normal distribution curve, and skewnorm distribution.

y_standard = norm.pdf(x_range, y_mean, y_std)

shape_param = 2

y_ks = skewnorm.pdf(x_range, a=y_skewness,
  loc=y_mean, scale=y_std / shape_param)

plt.plot(x_range, y_standard,
  label='Standard Normal')

plt.plot(x_range, y_ks, ls='-.',
  label='With Kurtosis and Skewness')

Python: Visualization: Statistic Properties: Kurtosis and Skewness

The result of the plot can be visualized as below:

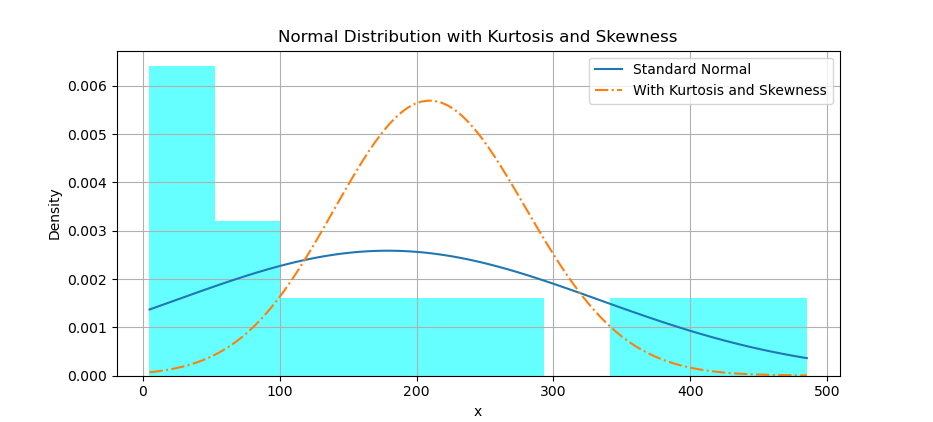
Python: Distribution Curve Plot: Kurtosis and Skewness

Actually, I’m not sure if I get the visual right. I still don;t know how this shape parameter works. Please consult your nearest statiscian to get the right interpretation.

You can obtain the interactive JupyterLab in this following link:

github.com/…/trend/68-plot-props.ipynb

Density with Seaborne

Seaborne can make a really pretty chart.

github.com/…/trend/69-sns.py

# Plot distribution of y with annotations
sns.set(style="whitegrid")
sns.displot(y_observed,
  bins=10, kde=True, rug=True)

Python: Visualization: Statistic Properties: Density with Seaborne

The result of the plot can be visualized as below:

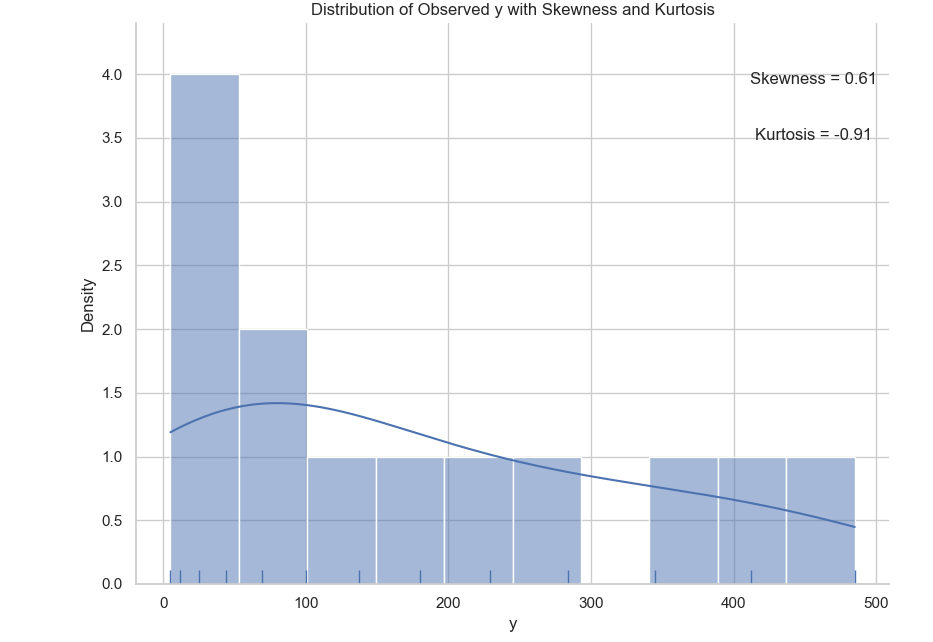
Python: Seaborne Plot: Density with Seaborne

You can obtain the interactive JupyterLab in this following link:

github.com/…/trend/69-sns.ipynb

What’s the Next Chapter 🤔?

Even with this cool matplotlib feature, we still need tool to make easy for us to visualize statistic properties. Fortunately, there is this seaborn library with ready to use plot chart, specifically made for statistics.

We are going to explore visualization again, further pretty plot with seaborn.

Consider progressing further by exploring the next topic: [ Trend - Properties - Additional ].