Trend - Properties

Trend: Introduction

Trend: Enhanced

Trend: Language

Local Group

Preface

Goal: Getting to know statistical properties, using worksheet formula step by step.

From equation, we can step-up to build statistic model in worksheet. We are going to explore formula to get statistical properties, manual calculation and also built-in method.

As a beginner, I must admit that was lost. I don’t know where to start. I read books, wiki, youtube channel, and finally find a way to craft analysis one by one. This why I create tabular calculation. After comparing with online calculator, I have confidence to write down my calculation in a blog.

Complete Worksheet

Although this looks complex. It is easy when you have a working example. This sheet looks long because I also add regression analysis and correlation.

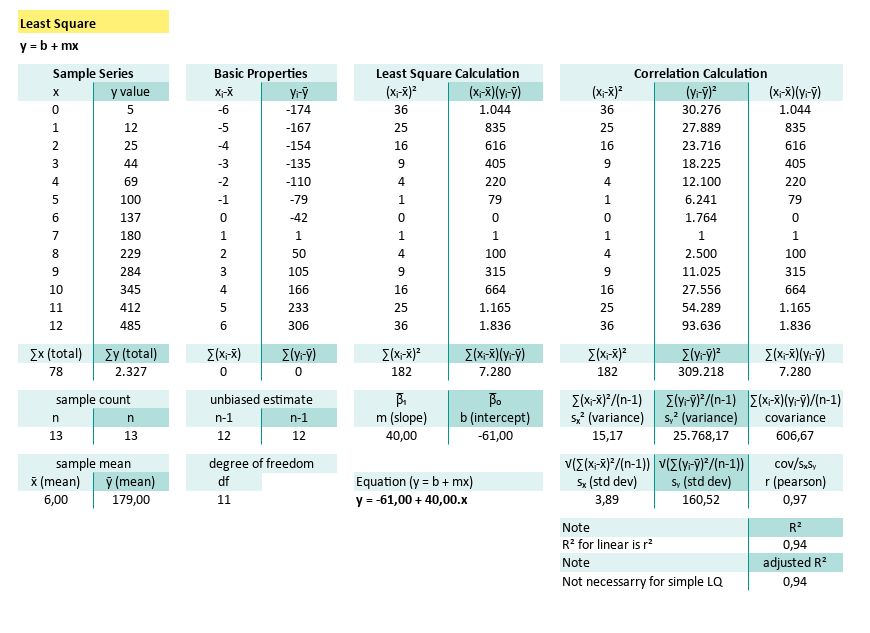
Trend: Worksheet: Least Square: Complete Worksheet

We will break down each section in this article. This article will use manual calculation. We will use built-in formula in the next article.

Worksheet Source

Playsheet Artefact

The Excel file is available, so you can have fun, modify as you want.

github.com/…/math/trend/examples-properties.xlsx

Known Values from Samples

Example Calculation

Let’s practice by example.

Supposed you have series of points from an observed samples, where x series in range B7:B19 and y series in C7:C19

(x, y) = [(0, 5), (1, 12), (2, 25), (3, 44), (4, 69), (5, 100), (6, 137), (7, 180), (8, 229), (9, 284), (10, 345), (11, 412), (12, 485)]

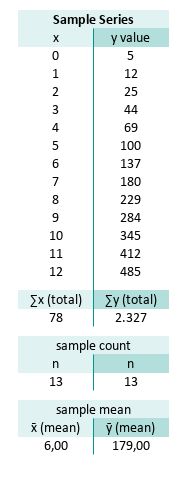
Trend: Worksheet: Known Values from Samples

We need to find:

$\begin{align*} \bar{x} = \frac{1}{n}\sum\limits_{i=1}^{n} x_i && \bar{y} = \frac{1}{n}\sum\limits_{i=1}^{n} y_i \\ \end{align*}$

With excel/calc, you can use count, sum, and average.

B22=SUM(B7:B19)
C22=SUM(C7:C19)

B26=COUNT(B7:B19)
C26=COUNT(C7:C19)

B30=AVERAGE(B7:B19)
C30=AVERAGE(C7:C19)

Or alternatively just divide the sum and the count.

B30=B22/B26
C30=C22/C26

The result of the statistic properties, total and mean are:

$\begin{align*} n = 13 && \sum x = 78 && \sum y = 2327 && \bar{x} = 6 && \bar{y} = 179 && \end{align*}$

Plot Result

We need a visualization so we can interpret the mean properties.

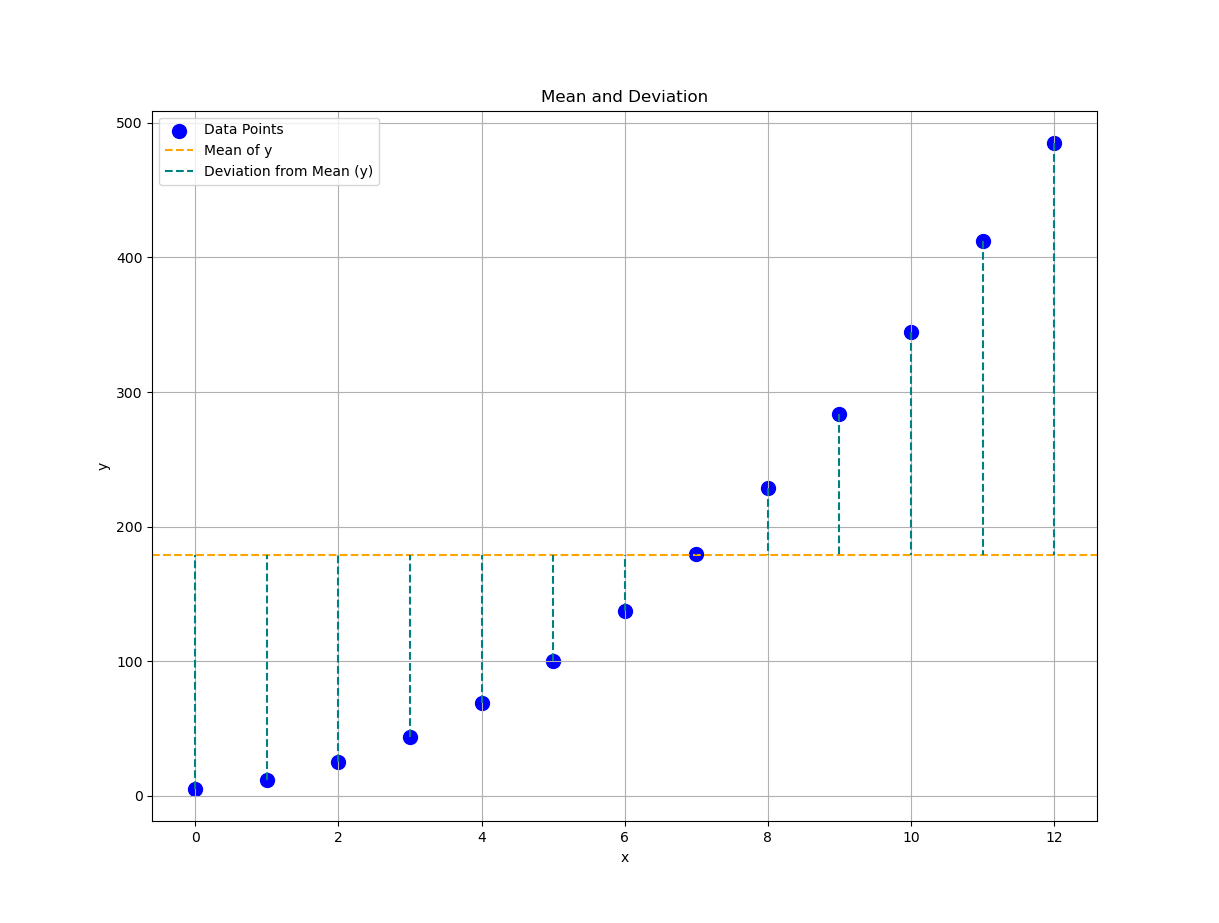
Trend: Plot: Variance

Basic Statistic Properties

We need to get the difference between observed data and the mean. Because we are going to use this variable in further calculation.

Trend: Worksheet: Basic Statistic Properties

For the series range E7:E19 and F7:F19 the formula are:

E7=B7-$B$30
F7=C7-$C$30
...
E19=B19-$B$30
F19=C19-$C$30

For samples, the unbiased estimate is (n-1). I’m just following the convention to use (n-1). The math behind is a hard topic, and beyond my knowledge, so I refused to explain.

$n - 1 = 12$

We haven’t need df (degree of freedom yet). I will explain this df later when required.

$df = n - k - 1 = 11$

In Excel/Calc we can write this as:

E26=COUNT(B7:B19)-1
F26=COUNT(C7:C19)-1

E30=COUNT(B7:B19)-2

Least Square Calculation

We have discuss in depth about the math behind in previous article. The slope (m) from the (y=mx+b) equation is:

$m = \frac{\sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum\limits_{i=1}^{n} (x_i - \bar{x})^2}$

What we need is to find each total these properties:

(xᵢ-x̄)²
(xᵢ-x̄)(yᵢ-ȳ)

Trend: Worksheet: Least Square Calculation

We need to find the nominator and the denominator.

$\begin{align*} \sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) && \sum\limits_{i=1}^{n} (x_i - \bar{x})^2 \\ \end{align*}$

For the series range H7:H19 (xᵢ-x̄)² and I7:I19 (xᵢ-x̄)(yᵢ-ȳ) the formula are:

H7=E7^2
I7=E7*F7
...
H19=E19^2
I19=E19*F19

The total ∑(xᵢ-x̄)² and ∑(xᵢ-x̄)(yᵢ-ȳ) can be defined as:

H22=SUM(H7:H19)
I22=SUM(I7:I19)

The result of the each total are:

$\begin{align*} \sum\limits_{i=1}^{n} (x_i - \bar{x})^2 &= 182 \\ \sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) &= 7280 \\ \end{align*}$

Now we got the m (slope) and b (intercept) as:

H26=I22/H22
I26=C30-H26*B30

The result of the statistic properties are:

$\begin{align*} m (slope) &= 40 \\ b (intercept) &= 61 \\ \end{align*}$

Finally we can get the equation (y = b + mx) as:

H30=CONCATENATE("y = ";TEXT(I26;"#.##0,00");" + ";TEXT(H26;"#.##0,00");".x")

Let’s write it in human form:

$y = -61 + 40x$

Again, you can see how easy it is to write down the equation in tabular spreadsheet form.

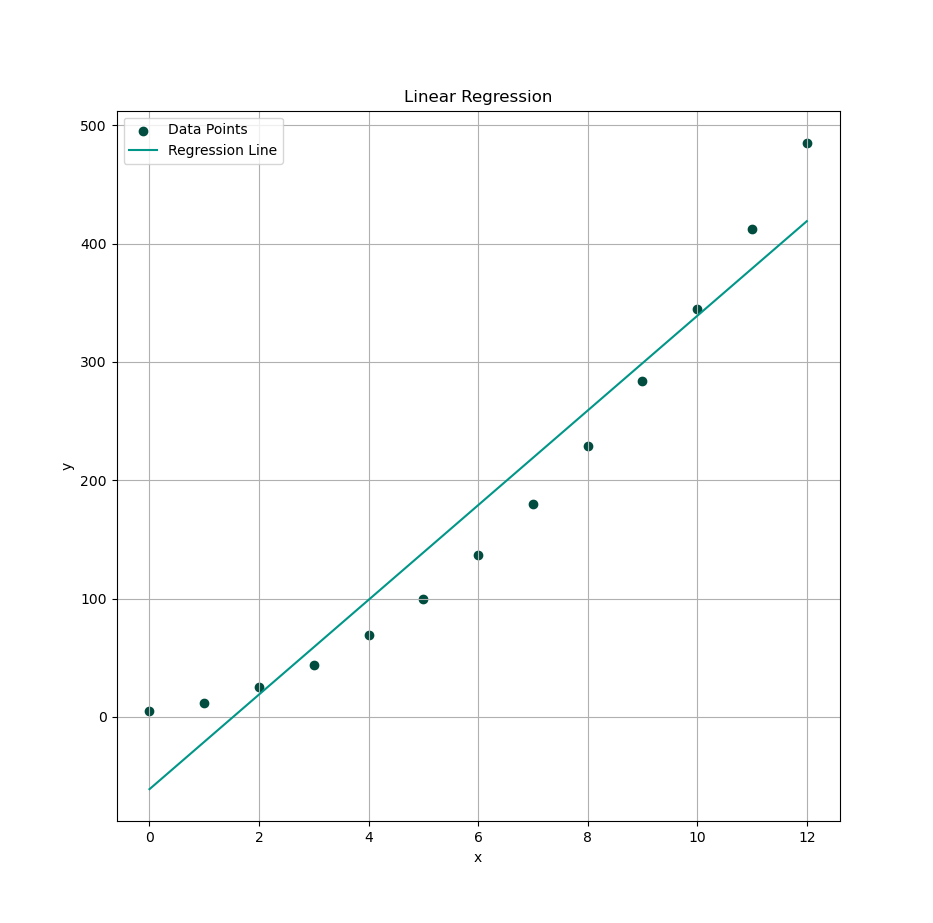
Plot Result

We need a visualization so we can interpret the properties above.

Trend: Plot: Linear Regression

Variance and Covariance

The equation of variance and covariance for a sample of data series (x, y) is given as follows:

$\begin{align*} s_x^2 &= \frac{1}{n-1}\sum\limits_{i=1}^{n} (x_i - \bar{x})^2 \\ s_y^2 &= \frac{1}{n-1}\sum\limits_{i=1}^{n} (y_i - \bar{y})^2 \\ \text{Cov}(x,y) &= \frac{1}{n-1}\sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \\ \end{align*}$

What we need is to find each total of each combination:

(xᵢ-x̄)²
(yᵢ-ȳ)²
(xᵢ-x̄)(yᵢ-ȳ)

For the series range K7:K19 (xᵢ-x̄)², L7:L19 (yᵢ-ȳ)² and M7:M19 (xᵢ-x̄)(yᵢ-ȳ) the formula are:

K7=E7^2
L7=F7^2
M7=E7*F7
...
K19=E19^2
L19=F19^2
M19=E19*F19

It is the same as before but we also add (yᵢ-ȳ)².

$\begin{align*} \sum\limits_{i=1}^{n} (x_i - \bar{x})^2 && \sum\limits_{i=1}^{n} (y_i - \bar{y})^2 && \sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \\ \end{align*}$

The total variation of the predictor, ∑(xᵢ-x̄)², (yᵢ-ȳ)² and ∑(xᵢ-x̄)(yᵢ-ȳ) can be defined as:

K22=SUM(K7:K19)
L22=SUM(L7:L19)
M22=SUM(M7:M19)

The result of the each total are:

$\begin{align*} \sum\limits_{i=1}^{n} (x_i - \bar{x})^2 &= 182 \\ \sum\limits_{i=1}^{n} (y_i - \bar{y})^2 &= 309218 \\ \sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) &= 7280 \\ \end{align*}$

Now we got the variance sₓ², sy² and also the covariance as:

K22=K22/E26
L22=L22/F26
M22=M22/E26

The result of the statistic properties are:

$\begin{align*} s_X^2 &= 15.17 \\ s_Y^2 &= 25768.17 \\ \text{Cov}(X,Y) &= 606.67 \\ \end{align*}$

The tabular spreadsheet can be shown as follows:

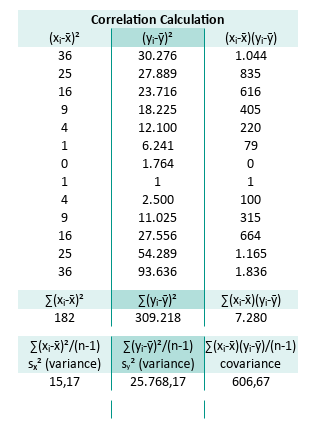
Trend: Worksheet: Correlation Calculation

Standard deviaton is square root of the variance.

Plot Result

We need a visualization so we can interpret the standard deviation properties against original observed y.

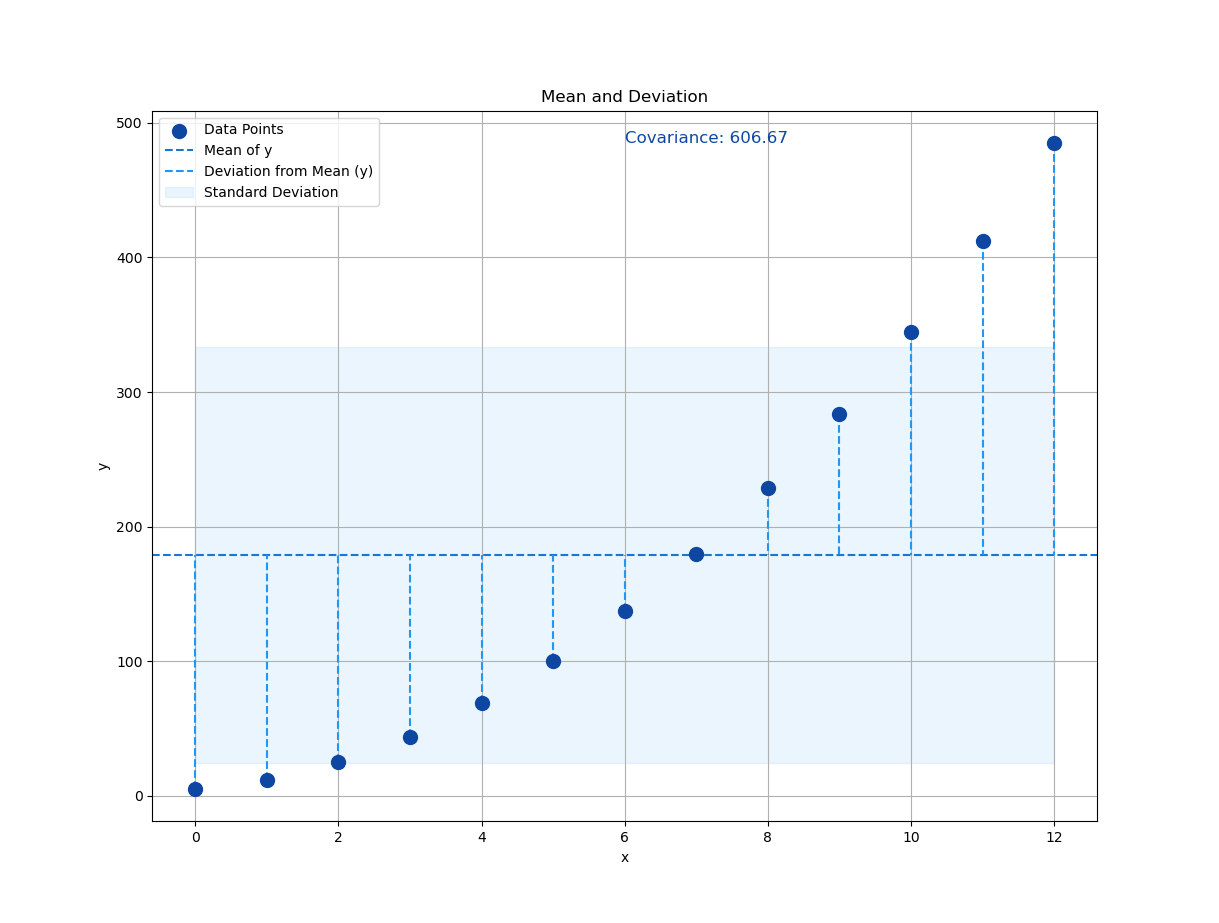
Trend: Plot: Variance

Correlation Calculation

From calculated properties above we can continue to standard deviation sₓ, sy, along with the r (pearson) value:

K30=SQRT(K26)
L30=SQRT(L26)
M30=M26/(K30*L30)

The result of the statistic properties are:

$\begin{align*} s_x &= \sqrt{s_X^2} &= && 3.89 \\ s_y &= \sqrt{s_Y^2} &= && 160.52 \\ r_{x,y} &= \frac{\text{Cov}(x,y)}{s_x . s_y} &= && 0,97 \\ \end{align*}$

Note that the pearson coefficient can be denoted in different form

r = cov/sₓsy
r = (∑(xᵢ-x̄).(yᵢ-ȳ))/√(∑(xᵢ-x̄)².∑(yᵢ-ȳ)²)

This way we can calculate the R square (R²) and also the adjusted R square. Note that R² for simple linear sample is the same as r². In this case R² = 0,9417. But the R² might be different for complex cases.

M33=M30^2

Also there is no need any adjusted R², for simple least square population. But for sample we need to adjust with k=1, for linear equation then adjusted R² = 0,9364.

M35=1-(1-M33)*(B26-1)/(B26-1-1)

We can have a look at the result, focusing on this part of following spreadsheet:

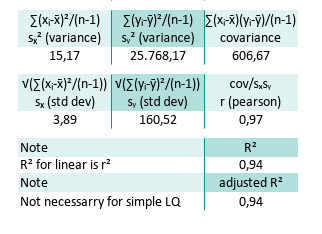
Trend: Worksheet: Residual Calculation

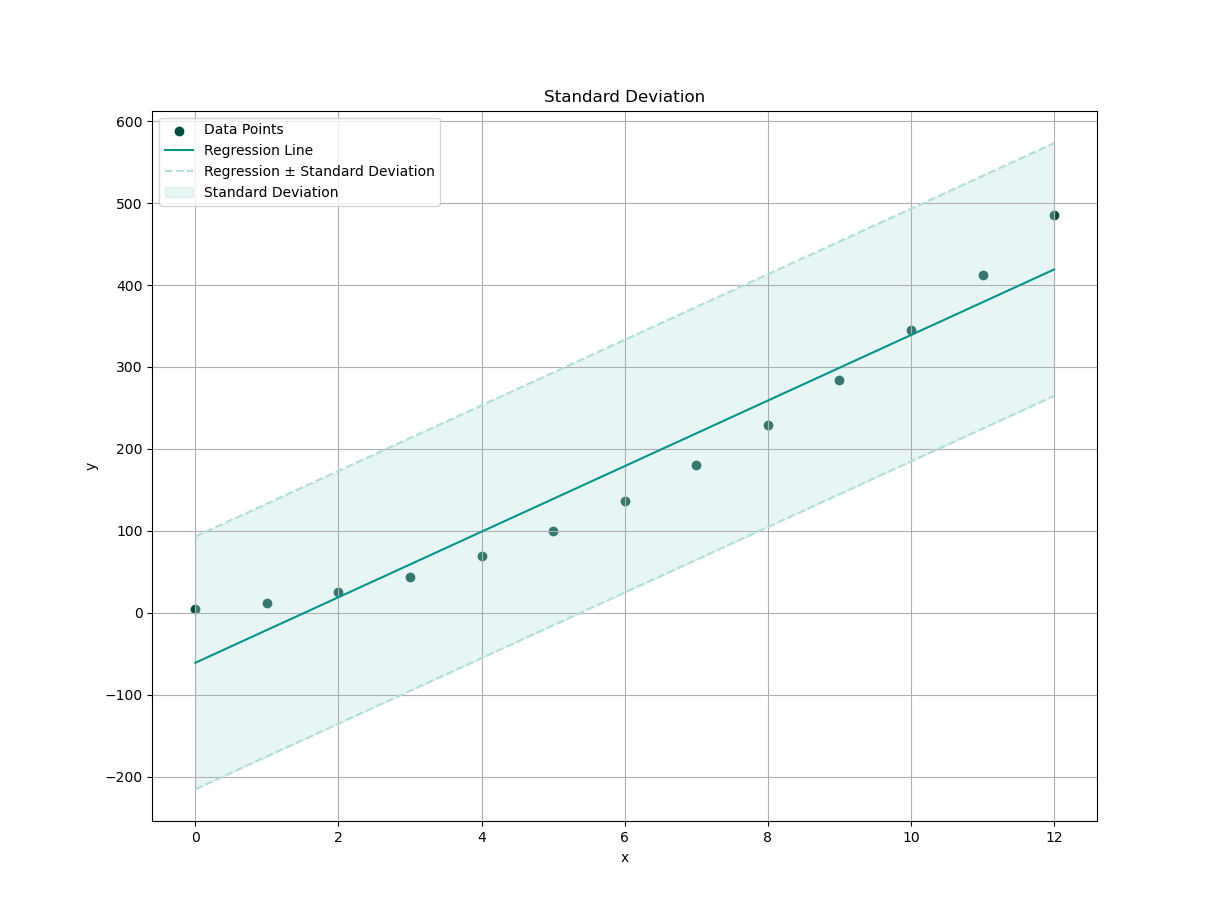
Plot Result

We need a visualization so we can interpret the standard deviation properties against predicted y.

Trend: Plot: Variance

Residual Calculation

From the coefficient of the linear least square,

m (slope)
b (intercept)

We can built our curve fitting equation (y = b + mx), and predict every yᵢ value.

For the series range O7:O19 fit(xᵢ), P7:P19 ϵᵢ (residual) and Q7:Q19 ϵᵢ² the formula are:

O7=$I$26+$H$26*B7
P7=C7-O7
M7=P7^2
...
O19=$I$26+$H$26*B19
P19=C19-O19
M19=P19^2

Note that we can use any curve fitting formula, such as quadratic, cubic and so on, but for this example we will use our linear one.

$\begin{align*} \hat{y}_i &= mx_i + b \\ e_i &= y_i - \hat{y}_i \\ \sum\limits_{i=1}^{n} (e_i)^2 &= \sum\limits_{i=1}^{n} (y_i - \hat{y}_i)^2 \\ \end{align*}$

The total of ϵᵢ² can be defined as:

Q22=SUM(Q7:Q19)

The result of the each total are:

$\sum\limits_{i=1}^{n} (e_i)^2 = 18018$

The tabular spreadsheet can be shown as follows:

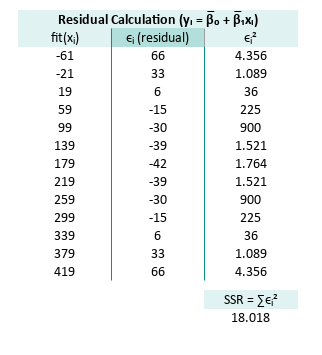
Trend: Worksheet: Residual Calculation

Plot Result

We need a visualization so we can interpret the residual properties.

Trend: Plot: Variance

Regressions Sum Square

There is this RSS

$\sum\limits_{i=1}^{n} (\hat{y}_i - \bar{y})^2$

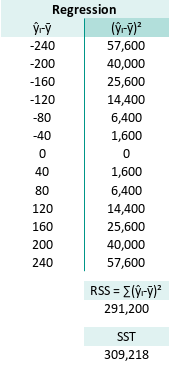
Trend: Worksheet: Regressions Sum Square

The SST (Sum Square Total) is

$SST = SSR + RSS$

While the SST has the same value with

$\sum\limits_{i=1}^{n} (y_i - \bar{y})^2$

t-value and p-value

We can finally calculate the t-value and p-value. This time we need degree of freedom. For linear equation k=1.

$df = n - k - 1 = 11$

In Excel/Calc we can write this as:

E30=COUNT(B7:B19)-2

Mean Squared Error can be calculated as follows:

$MSE = \frac{SSE}{df}$

In Excel/Calc we can write this as:

=Q22/$E$30

The standard error of the slope (SE(β1)) in a linear regression model is related to the Mean Squared Error (MSE) as follows:

$SE(\beta_1) = \sqrt{\frac{MSE}{\sum_{i=1}^{n}(x_i - \bar{x})^2}}$

In Excel/Calc we can write this as:

=SQRT(Q25/K22)

The t-value for the slope coefficient (β1) is computed as the ratio of the estimated slope (βˉ1) to the standard error of the slope (SE(β1)). This t-value will be used to test the null hypothesis that the true slope coefficient is equal to zero.

$t = \frac{\bar{\beta}_1}{SE(\beta_1)}$

In Excel/Calc we can write this as:

=H26/Q30

And finally we can find the p-value for two tail test.

$p = 2 \times P(T > |t|)$

This is to complex for manual calculation, so I use built-in formula instead.

=T.DIST.2T(Q35;$E$30)

The result of the statistic properties are:

$\begin{align*} df &= 11 \\ MSE &= 1638 \\ SE(\beta_1) &= 3.00 \\ t-value &= 13.33 \\ p-value &= 0,0000000391 \\ \end{align*}$

We can have a look at the result, focusing on this part of following spreadsheet:

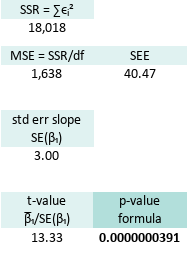
Trend: Worksheet: p value

We have a good confidence in our curve fitting function.

Alternative Worksheet

Above worksheet is not the only tabular method to describe, low level calculation of regression and correlation. We can use any tabular method as shown below:

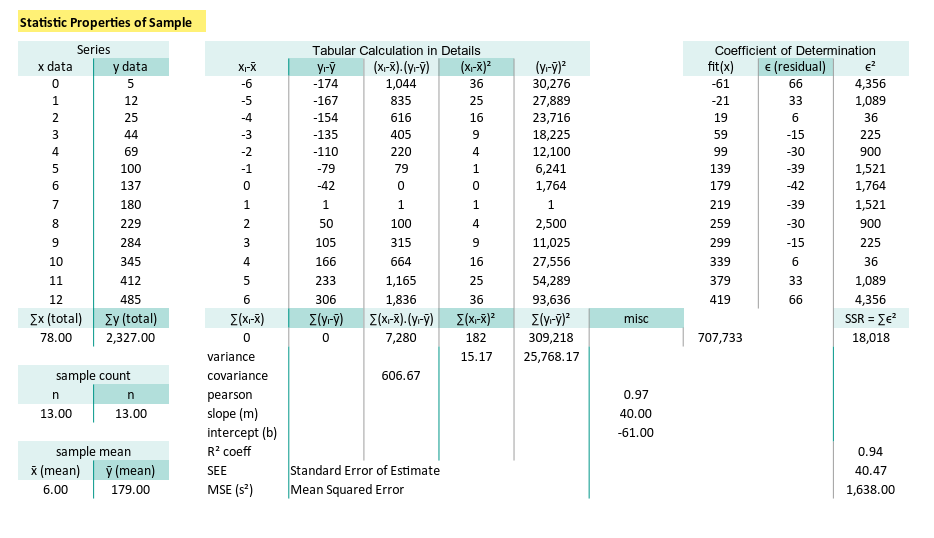
Trend: Worksheet: Correlation: Tabular Worksheet

Built In Formula

We are going to explore built-in formula in spreadsheet as shown in below picture. The tabular calculation above is not the only way. This is why we have to explore further in alternative tabular spreadsheet. At the end we are also going to explore statistical library in python.

Worksheet Source

Playsheet Artefact

The Excel file is available, so you can have fun, modify as you want.

github.com/…/math/trend/examples-properties.xlsx

Data Series Source

Consider this series of points in this worksheet:

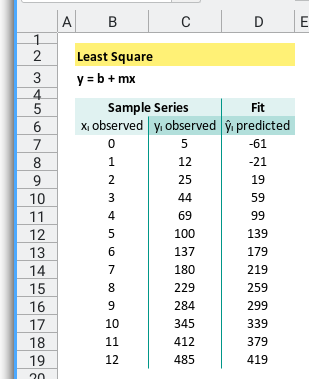
Trend: Worksheet: Built-in Formula: Data Series

xᵢ observed: B7:B19,
yᵢ observed: C7:C19,
ŷᵢ predicted: D7:D19 calculated from m and b.

Named Range

To make the equation less cryptic, we can define named range. This can be done in both Excel and Calc:

Trend: Worksheet: Built-in Formula: Named Range

Lets, name our range as follows:

B7:B19: x_observed.
C7:C19: y_observed.
D7:D19: y_predicted.

Using Array Operation

We can rebuild tabular woksheet from previous article, into a simple one using Excel/Calc formula with the help of SUMSQ formula.

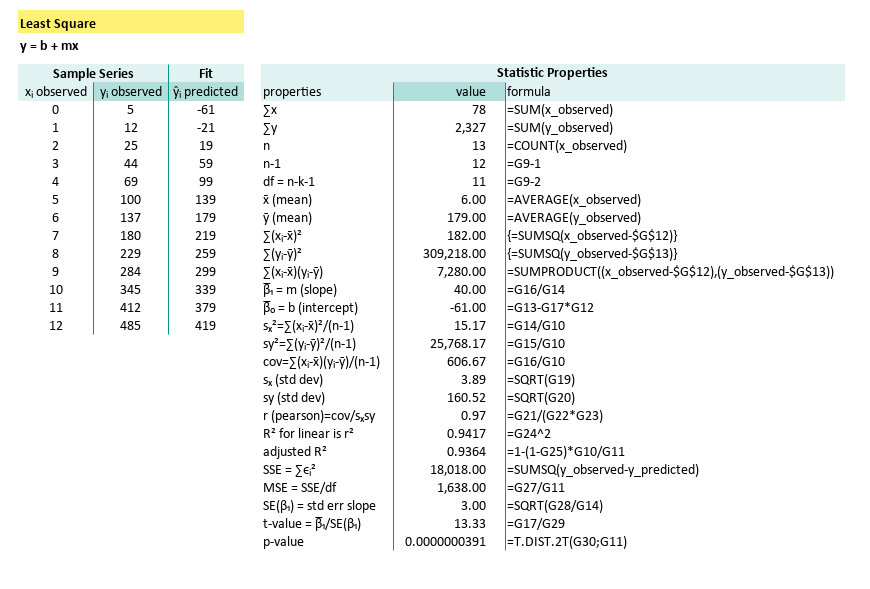
Trend: Worksheet: Built-in Formula: Array

Here the predicted value of ŷᵢ in D7:D19 are calculated from m ($G$17) and b ($G$18).

The complete formula can be shown here:

properties	formula
∑x	=SUM(x_observed)
∑y	=SUM(y_observed)
n	=COUNT(x_observed)
n-1	=G9-1
df = n-k-1	=G9-2
x̄ (mean)	=AVERAGE(x_observed)
ȳ (mean)	=AVERAGE(y_observed)
∑(xᵢ-x̄)²	{=SUMSQ(x_observed-$G$12)}
∑(yᵢ-ȳ)²	{=SUMSQ(y_observed-$G$13)}
∑(xᵢ-x̄)(yᵢ-ȳ)	=SUMPRODUCT((x_observed-$G$12),(y_observed-$G$13))
β̅₁ = m (slope)	=G16/G14
β̅₀ = b (intercept)	=G13-G17*G12
sₓ²=∑(xᵢ-x̄)²/(n-1)	=G14/G10
sy²=∑(yᵢ-ȳ)²/(n-1)	=G15/G10
cov=∑(xᵢ-x̄)(yᵢ-ȳ)/(n-1)	=G16/G10
sₓ (std dev)	=SQRT(G19)
sy (std dev)	=SQRT(G20)
r (pearson)=cov/sₓsy	=G21/(G22*G23)
R² for linear is r²	=G24^2
adjusted R²	=1-(1-G25)*G10/G11
SSE = ∑ϵᵢ²	{=SUMSQ(y_observed-D7:D19)}
MSE = SSE/df	=G27/G11
SE(β₁) = std err slope	=SQRT(G28/G14)
t-value = β̅₁/SE(β₁)	=G17/G29
p-value	=T.DIST.2T(G30;G11)

I believe that will reduced the need of tabular worksheet.

Using Statistic Formula

Furthermore we can use statistic formula. Since we want to make in different worksheet, then we have to define different range name.

Lets, name our range as follows:

B7:B19: x_sample.
C7:C19: y_sample.
D7:D19: y_fit.

The built in formula for each statistic properties are as follows:

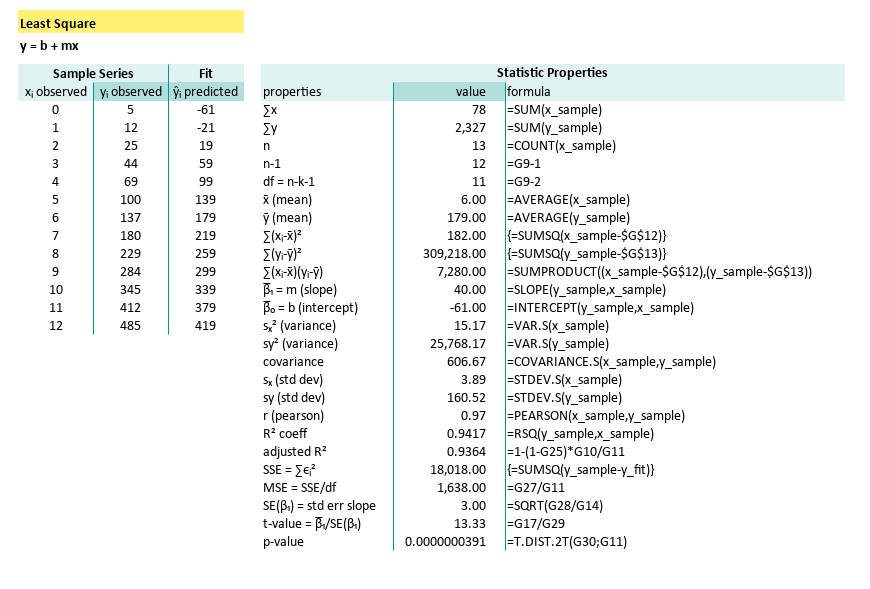
Trend: Worksheet: Built-in Formula: Statistic

properties	formula
∑x	=SUM(x_sample)
∑y	=SUM(y_sample)
n	=COUNT(x_sample)
n-1	=G9-1
df = n-k-1	=G9-2
x̄ (mean)	=AVERAGE(x_sample)
ȳ (mean)	=AVERAGE(y_sample)
∑(xᵢ-x̄)²	{=SUMSQ(x_sample-$G$12)}
∑(yᵢ-ȳ)²	{=SUMSQ(y_sample-$G$13)}
∑(xᵢ-x̄)(yᵢ-ȳ)	=SUMPRODUCT((x_sample-$G$12),(y_sample-$G$13))
β̅₁ = m (slope)	=SLOPE(y_sample,x_sample)
β̅₀ = b (intercept)	=INTERCEPT(y_sample,x_sample)
sₓ² (variance)	=VAR.S(x_sample)
sy² (variance)	=VAR.S(y_sample)
covariance	=COVARIANCE.S(x_sample,y_sample)
sₓ (std dev)	=STDEV.S(x_sample)
sy (std dev)	=STDEV.S(y_sample)
r (pearson)	=PEARSON(x_sample,y_sample)
R² coeff	=RSQ(y_sample,x_sample)
adjusted R²	=1-(1-G25)*G10/G11
SSE = ∑ϵᵢ²	{=SUMSQ(y_sample-y_fit)}
MSE = SSE/df	=G27/G11
SE(β₁) = std err slope	=SQRT(G28/G14)
t-value = β̅₁/SE(β₁)	=G17/G29
p-value	=T.DIST.2T(G30;G11)

The parameter required for each statistic formula is clear now. This make our worksheet easier to be read. Reducing error in analysis.

Pearson Coeffecient

Excel/Calc has a built-in formula for Pearson coefficient value:

=PEARSON(B7:B19;C7:C19)

The pearson coefficient itself is defined as

$r_{x,y} \frac{\text{Cov}(x,y)}{s_x . s_y} \\$

The Excel/Calc formula can be rewritten as:

=COVARIANCE.P(B7:B19, C7:C19) / (STDEV.P(B7:B19) * STDEV.P(C7:C19))

The Pearson correlation coefficient can also be expressed as follows:

$r = \frac{\sum (x_i - \bar{x}) \cdot (y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \cdot \sum (y_i - \bar{y})^2}}$

Sometimes you want to check if your equation right. Again, the Excel/Calc formula can be rewritten as follows, and having the same result.

= (SUM((B7:B19 - AVERAGE(B7:B19)) * (C7:C19 - AVERAGE(C7:C19)))) 
/ (SQRT(SUM((B7:B19 - AVERAGE(B7:B19))^2) * SUM((C7:C19 - AVERAGE(C7:C19))^2)))

Now you know, how helpful the built-in formula is, compared to this complex formula above.

R Square

Excel/Calc has a built-in formula for R Square (R²):

=RSQ(C7:C19;B7:B19)

The R Square (R²) for simple linear regression can be expressed as follows:

$\begin{align*} r_{x,y} &= \frac{\text{Cov}(x,y)}{s_x . s_y} \\ R^2 &= r_{x,y}^2 \end{align*}$

The general R Square (R²) is defined as:

$R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2}$

Or furthermore, we can go low-level.

$R^2 = 1 - \frac{\sum (y_i - (\hat{\beta}_1 x_i + \hat{\beta}_0))^2}{\sum (y_i - \bar{y})^2}$

Again, the Excel/Calc formula can be rewritten as:

=1-SUM((C7:C19 - (B7:B19*G22+G24))^2)/SUM((C7:C19 - H9)^2)

The way you manage the calculation is depend on your situation. Most of the time we can use simple rsq formula, but sometimes we need to go low level, for use with programming or just intellectual curiosity.

Let’s see how RSQ behave in non-linear curve fitting discussed later on.

Comparation

If you wish, you can have comparation, between manual formula and built-in formula as shown below:

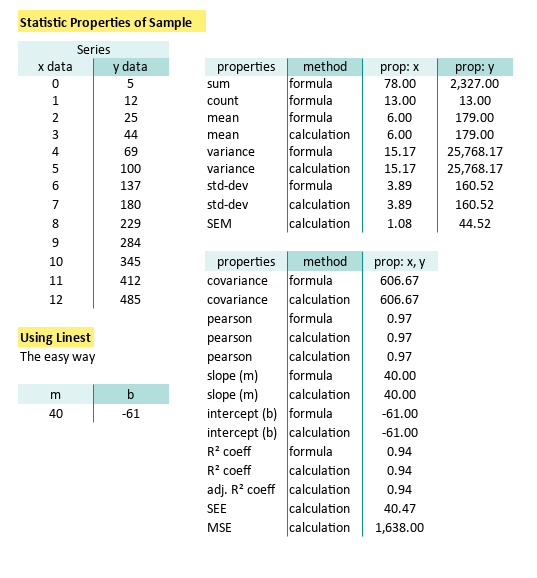
Trend: Worksheet: Correlation: Built-in Worksheet

Now you are ready to make statistical model, in your worksheet to suit your specific needs.

How you make the model is up to you.

What Lies Ahead 🤔?

That above is a complex way to get the result. Of course there is a simple way get the result. In order to have a spreadsheet model that suitable for daily basis, we need to explore different calculation method.

Consider diving into the next step by exploring [ Trend - Properties - Python Tools ].

Trend - Properties - Formula

Preface

Complete Worksheet

Worksheet Source

Known Values from Samples

Plot Result

Basic Statistic Properties

Least Square Calculation

Plot Result

Variance and Covariance

Plot Result

Correlation Calculation

Plot Result

Residual Calculation

Plot Result

Regressions Sum Square

t-value and p-value

Alternative Worksheet

Built In Formula

Worksheet Source

Data Series Source

Named Range

Using Array Operation

Using Statistic Formula

Pearson Coeffecient

R Square

Comparation

What Lies Ahead 🤔?