Trend - Polynomial Interpolation

Trend: Introduction

Trend: Enhanced

Trend: Language

Local Group

Preface

Goal: Connect the dots perfectly with interpolation.

Curve fitting is not the only target that you want to achieve. We might just want to connect the dots perfectly. This is called interpolation.

Unlike curve fitting, interpolation require the curve to pass through all the given data points. We can use polynomial method to connect a few data points. This method use minimal required point to calculate the equation for example:

Two points for linear equation.
Three points for quadratic equation.
Four points for cubic equation.

There is even an easier way to obtain linear equation. It is by calculating the slope.

Please note that when conducting interpolation in practical applications, curve fitting isn’t the sole method available. There are also the option to utilize multiple straight lines, connecting points from one to another, without necessitating of curve fitting at all.

Worksheet Source

Playsheet Artefact

The worksheet provided is ready to used for daily problem solving.

Polynomial: Worksheet: Cubic: Matrix Formula

This workbook containing multiple sheet, so you can choose any method that suit for you.

Spreadsheet: Workbook with Multiple Worksheet

The Excel file is available, so you can have fun, modify as you want.

github.com/…/math/trend/10-curve-fitting.xlsx

1: Straight Line from Two Points

Calculating Slope

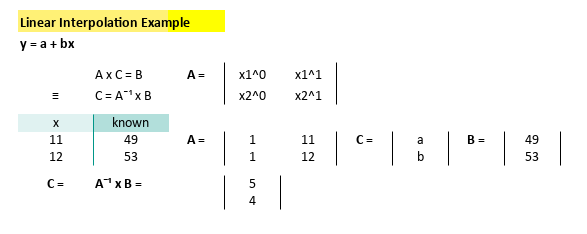
If all you need is just conneting two point, you should use simple method instead of the complex one. Stay away from polynomial method, and just use this slope equation.

The Math Behind

The equation of linear trend for staright line is simple.

$y = mx + a$

To calculate the slope you can just measure the difference for both y and x.

$m = \frac{{\Delta y}}{{\Delta x}}$

For two points, the slope become y2-y1, and x2-x1.

$m = \frac{{y_2 - y_1}}{{x_2 - x_1}}$

Then we can finally get the a variable.

$a = y_1 - mx_1$

The variable names is commonly named as:

m: slope, and
a: intercept.

The notation can be different from book to book. But they have the same meaning. Such this below example:

$y = b + mx$

You might even see the cryptic form as below, for curve fitting with many samples data.

$y_i = \bar{\beta}_0 + \bar{\beta}_1 x_i$

They are all serve simple straight lines.

Getting Coefficient

Supposed you have two pairs of point

p1 = (11, 49), and
p2 = (12, 53)

Polynomial: Worksheet: Straight Line: Getting Coefficient

You can get the coefficient as

m = 5, and
a = 4

Predicting Values

Now you can predict the interpolation value for example [0, 5, 12]

Polynomial: Worksheet: Straight Line: Predicting Values

This will get this pairs of point:

(x = 0, y = 5),
(x = 5, y = 25),
(x = 12, y = 53),

And so on.

Polynomial Interpolation: Linear

Minimum Two Points

Matrix Equation

Getting unknown Coefficient value

Supposed we want to connect two points.

$\begin{align*} p_0 &= (x_0, y_0) &= (11, 49) \\ p_1 &= (x_1, y_1) &= (12, 53) \\ \end{align*}$

A system of linear equations can be represented as a matrix equation

$\begin{array}{cc} \begin{bmatrix} y_0 \\ y_1 \\ \end{bmatrix} = \begin{bmatrix} 1 & x_0 \\ 1 & x_1 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 49 \\ 53 \\ \end{bmatrix} = \begin{bmatrix} 1 & 11 \\ 1 & 12 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ \end{bmatrix} \end{array}$

This matrix can be represented as variable below:

$A\mathbf{C} = \mathbf{B}$

We are going to solve the formula above using this equation

$\begin{aligned} && A \times \mathbf{C} &= \mathbf{B} \\ \Rightarrow && \mathbf{C} &= A^{-1} \times \mathbf{B} \\ \end{aligned}$

You can use spreadsheet using minverse formula.

$A^{-1} = \begin{bmatrix} 12 & -11 \\ -1 & 1 \\ \end{bmatrix}$

And solve this matrix equation and get below coefficient result:

$\mathbf{C} = A^{-1} \times \mathbf{B} = \begin{bmatrix} 5 \\ 4 \\ \end{bmatrix}$

The detail is:

$\begin{aligned} \begin{bmatrix} 12 & -11 \\ -1 & 1 \\ \end{bmatrix} \times \begin{bmatrix} 49 \\ 53 \\ \end{bmatrix} &= \begin{bmatrix} 12\times49 - 11\times53 \\ -1\times49 + 1\times53 \\ \end{bmatrix} \\ &= \begin{bmatrix} 588 - 583 \\ -49 + 53 \\ \end{bmatrix} \\ &= \begin{bmatrix} 5 \\ 4 \\ \end{bmatrix} \end{aligned}$

With coefficient above we can write the linear equation as below:

$y = 5 + 4x$

Worksheet

Getting unknown Y-Value

With spreadsheet, we can write down the equation, as below to get the coefficient:

Polynomial: Worksheet: Straight Line: Getting Coefficent

The formula is something like below:

=MMULT(MINVERSE(E9:F10);J9:J10)

Now we can easily get the predicted value using interpolation above.

Polynomial: Worksheet: Straight Line: Predicting Values

Polynomial Interpolation: Quadratic

Minimum Three Points

With the same method as linear equation, we can do the the quadratic equation.

Matrix Equation

Getting unknown Coefficient value

Supposed we want to connect three points.

$\begin{align*} p_0 &= (x_0, y_0) &= (10, 345) \\ p_1 &= (x_1, y_1) &= (11, 412) \\ p_2 &= (x_2, y_2) &= (12, 485) \\ \end{align*}$

A system of quadratic equations can also be represented as a matrix equation

$\begin{array}{cc} \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ \end{bmatrix} = \begin{bmatrix} 1 & x_0 & {x_0}^2 \\ 1 & x_1 & {x_1}^2 \\ 1 & x_2 & {x_2}^2 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 345 \\ 412 \\ 485 \\ \end{bmatrix} = \begin{bmatrix} 1 & 10 & 100 \\ 1 & 11 & 121 \\ 1 & 12 & 144 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} \end{array}$

This matrix also can be represented as variable. Again, we are going to solve the formula above using this equation

$\begin{aligned} && A\mathbf{C} &= \mathbf{B} \\ \Rightarrow && \mathbf{C} &= A^{-1} \mathbf{B} \\ \end{aligned}$

You can use spreadsheet using minverse formula.

$A^{-1} = \begin{bmatrix} 66 & -20 & 55 \\ -11.5 & 22 & -10.5 \\ 0.5 & -1 & 0.5 \\ \end{bmatrix}$

And solve this matrix equation and get below coefficient result:

$\mathbf{C} = A^{-1} \mathbf{B} = \begin{bmatrix} 5 \\ 4 \\ 3 \\ \end{bmatrix}$

With coefficient above we can write the linear equation as below:

$y = 5 + 4x + 3x^2$

Worksheet

Getting unknown Y-Value

With spreadsheet, we can write down the equation, as below to get the coefficient:

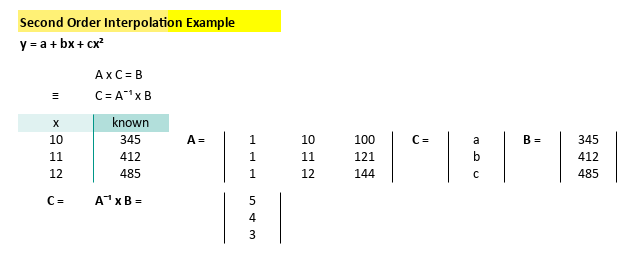
Polynomial: Worksheet: Quadratic: Getting Coefficent

The formula is something like below:

=MMULT(MINVERSE(E9:G11);K9:K11)

Now we can easily get the predicted value using interpolation above.

Polynomial: Worksheet: Quadratic: Predicting Values

Polynomial Interpolation: Cubic

Minimum Four Points

With the same method as linear equation and quadratic equation, we can do the the cubic equation.

Matrix Equation

Getting unknown Coefficient value

Supposed we want to connect three points.

$\begin{align*} p_0 &= (x_0, y_0) &= &(9, 1742) \\ p_1 &= (x_1, y_1) &= &(10, 2345) \\ p_2 &= (x_2, y_2) &= &(11, 3074) \\ p_3 &= (x_3, y_3) &= &(12, 3941) \\ \end{align*}$

A system of cubic equations can be represented as a matrix equation

$\begin{array}{cc} & \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \end{bmatrix} = \begin{bmatrix} 1 & x_0 & {x_0}^2 & {x_0}^3 \\ 1 & x_1 & {x_1}^2 & {x_0}^3 \\ 1 & x_2 & {x_2}^2 & {x_0}^3 \\ 1 & x_3 & {x_3}^2 & {x_0}^3 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ \end{bmatrix} \\ \Rightarrow & \begin{bmatrix} 1742 \\ 2345 \\ 3074 \\ 3941 \\ \end{bmatrix} = \begin{bmatrix} 1 & 9 & 81 & 729 \\ 1 & 10 & 100 & 1000 \\ 1 & 11 & 121 & 1331 \\ 1 & 12 & 144 & 1728 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ \end{bmatrix} \end{array}$

This matrix also can be represented as variable. Again, we are going to solve the formula above using this equation

$\begin{aligned} && A\mathbf{C} &= \mathbf{B} \\ \Rightarrow && \mathbf{C} &= A^{-1} \mathbf{B} \\ \end{aligned}$

You can still use spreadsheet using minverse formula, to solve this matrix equation and get below coefficient result:

$\mathbf{C} = A^{-1} \mathbf{B} = \begin{bmatrix} 5 \\ 4 \\ 3 \\ 2 \\ \end{bmatrix}$

With coefficient above we can write the linear equation as below:

$y = 5 + 4x + 3x^2 + 2x^3$

Worksheet

Getting unknown Y-Value

With spreadsheet, we can write down the equation, as below to get the coefficient:

Polynomial: Worksheet: Cubic: Getting Coefficent

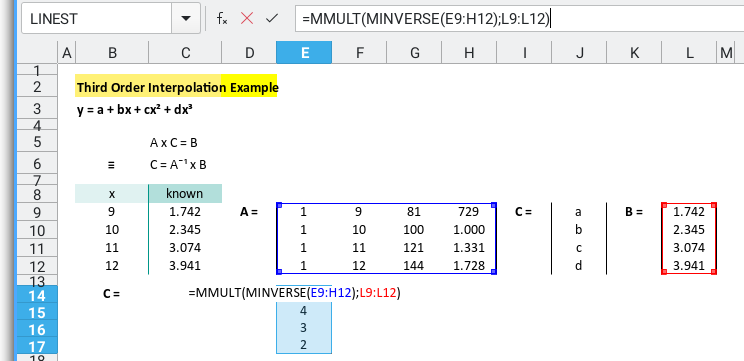
The formula is something like below:

=MMULT(MINVERSE(E9:H12);L9:L12)

Now we can easily get the predicted value using interpolation above.

Polynomial: Worksheet: Cubic: Predicting Values

What’s Our Next Endeavor 🤔?

Polynomial curve fitting using the same basic equation as above, but using more data. In real life most data are dispersed, and do not connect perfectly between points. All we need to do is adjust the equation a bit, and also adjust the previous polyfit into manual matrix calculation.

For a hands-on experience and a deeper grasp of these concepts, let’s explore further in [ Trend - Polynomial Algebra ].