Preface
Goal: A quick glance to the open source PSPPire.
I would really like to explore PSPPire. PSPP is the open source version of SPSS.
We need to verify the result of our previous excel and python, with a real statistic application.
Using PSPPire
The first time using PSPPire is easy as long as you know this interface.
User Interface
The PSPP itself is just a TUI (terminal user interface).
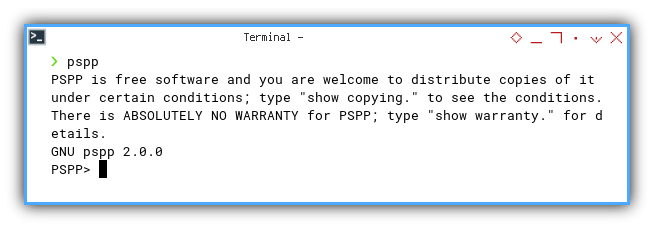
You need PSPPire to run the GUI (graphical user interface)
Import Data
We can import our previous CSV series using Import Data menu.
For example this CSV file
x, y
0, 5
1, 12
2, 25
3, 44
4, 69
5, 100
6, 137
7, 180
8, 229
9, 284
10, 345
11, 412
12, 485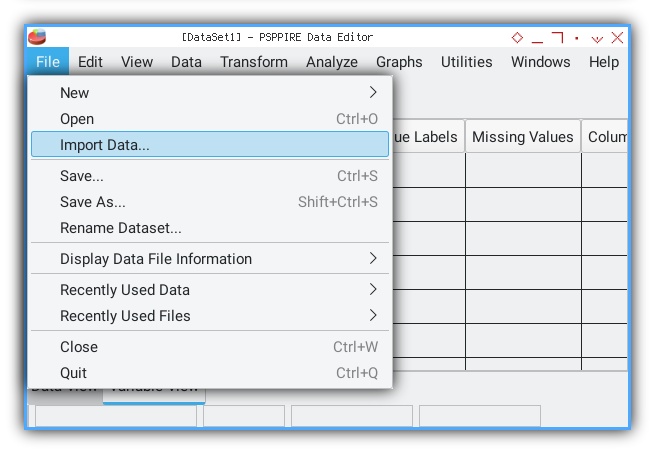
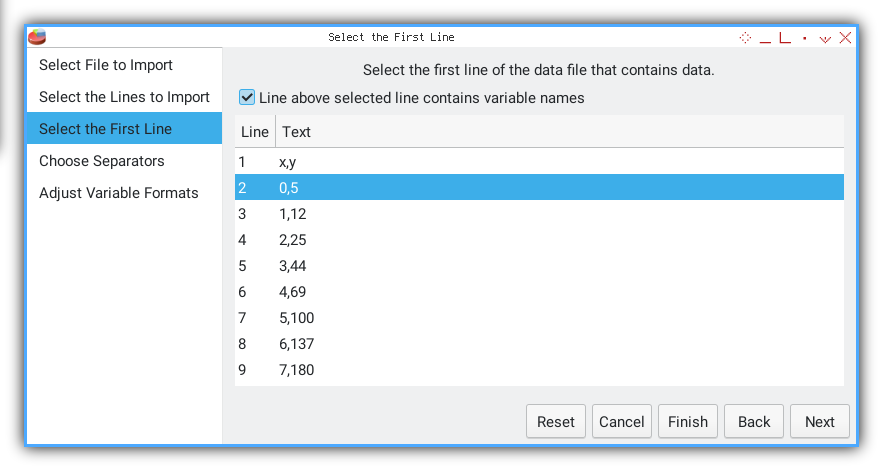
We need to follow required procedure, such as selecting rows.
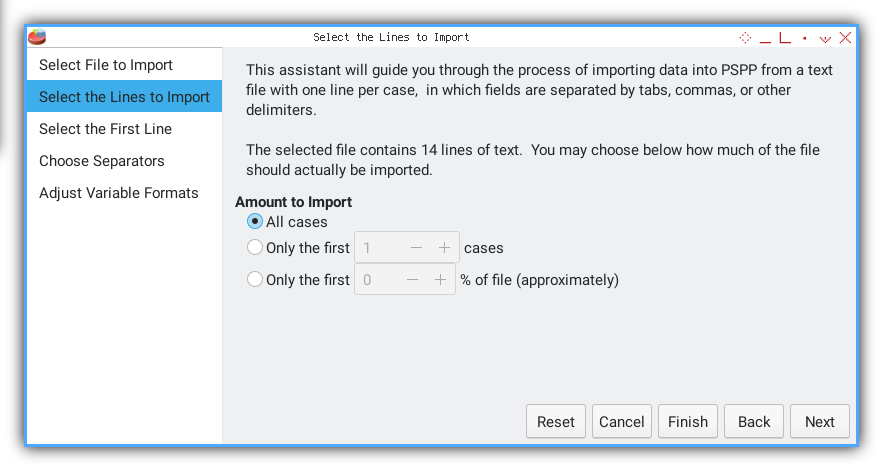
This part, I choose the second line.
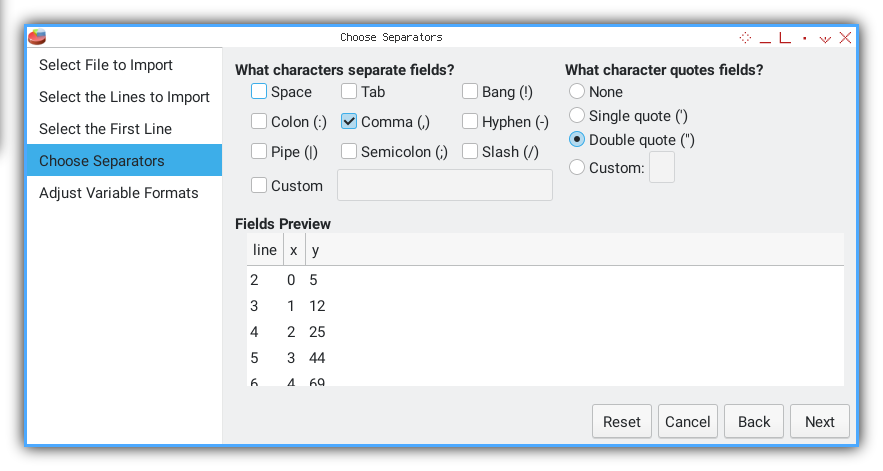
Separator.
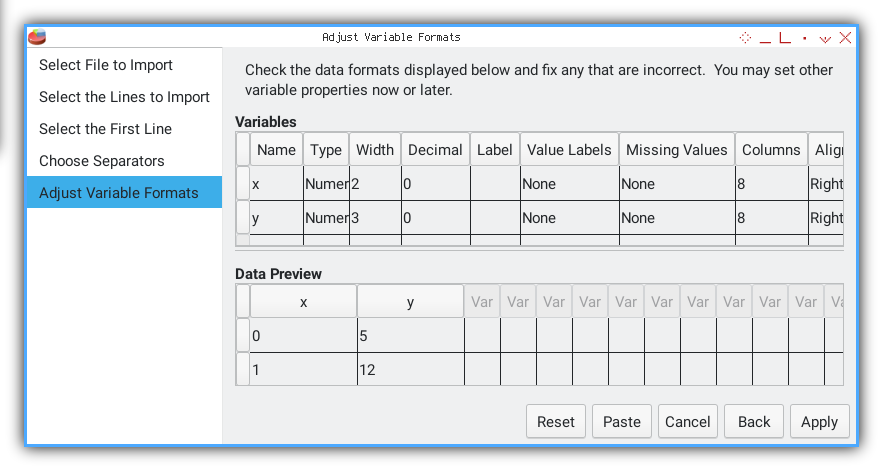
Variable format.
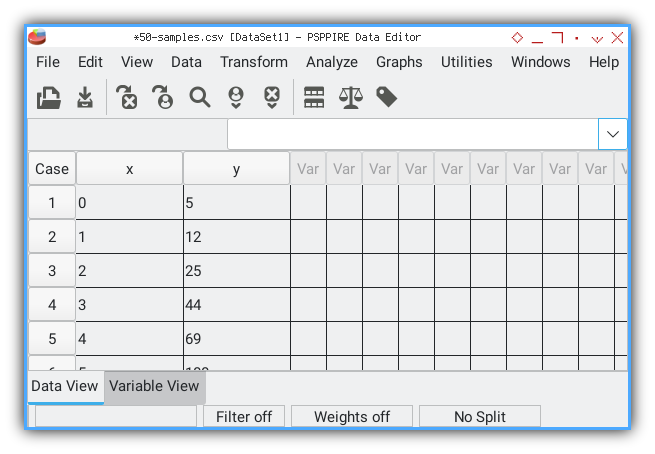
And you are done. You may switch to data view.
There will be other window popping up. This is the output viewer.
GET DATA
/TYPE=TXT
/FILE="/home/epsi/50-samples.csv"
/ARRANGEMENT=DELIMITED
/DELCASE=LINE
/FIRSTCASE=2
/DELIMITERS=","
/VARIABLES=
x F2.0
y F3.0.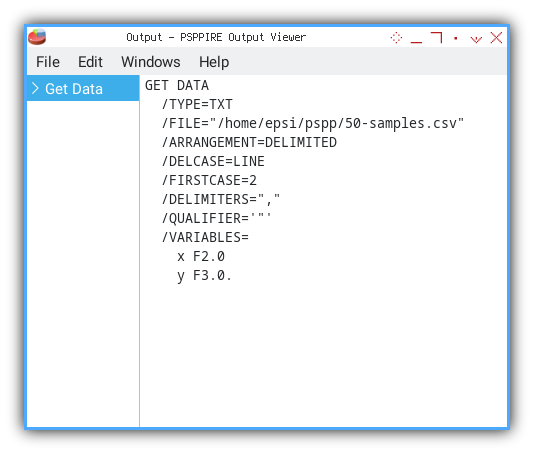
The output above is the command line.
Frequency Analysis
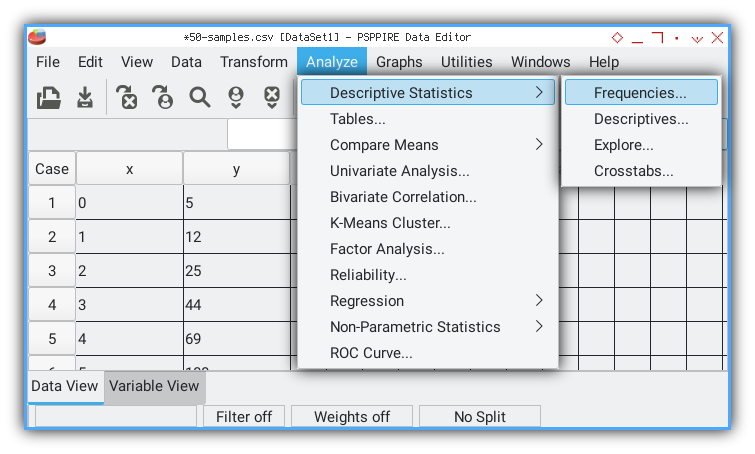
Now you can do analysis easily.
PSPPire
You can start by choosing anaylisis menu.
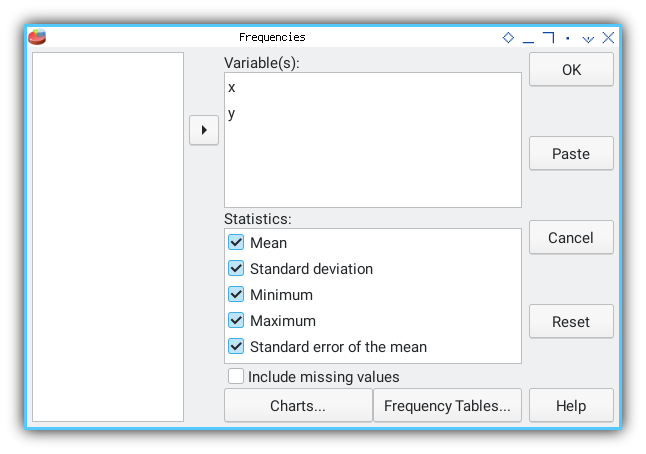
Fill the necessary dialog. Click OK.
And voila, the output viewer.
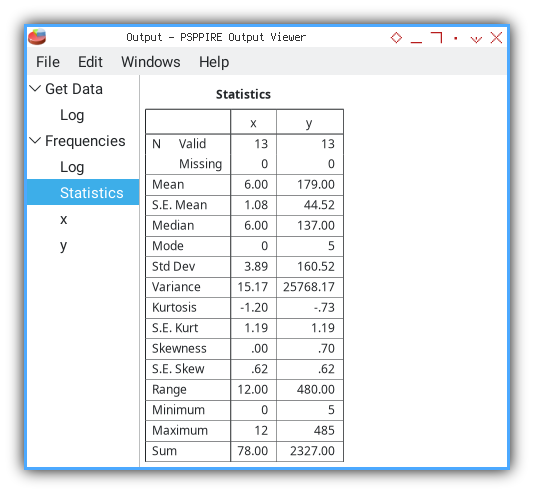
The output is similar with this below. The first text is the command line.
FREQUENCIES
/VARIABLES= x y
/FORMAT=AVALUE TABLE
/STATISTICS=ALL.Followed by tabular data of statistical properties.
Statistics
โญโโโโโโโโโโฌโโโโโโฌโโโโโโโโโฎ
โ โ x โ y โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โN Valid โ 13โ 13โ
โ Missingโ 0โ 0โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โMean โ 6.00โ 179.00โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โS.E. Meanโ 1.08โ 44.52โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โMedian โ 6.00โ 137.00โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โMode โ 0โ 5โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โStd Dev โ 3.89โ 160.52โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โVariance โ15.17โ25768.17โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โKurtosis โ-1.20โ -.73โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โS.E. Kurtโ 1.19โ 1.19โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โSkewness โ .00โ .70โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โS.E. Skewโ .62โ .62โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โRange โ12.00โ 480.00โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โMinimum โ 0โ 5โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โMaximum โ 12โ 485โ
โโโโโโโโโโโผโโโโโโผโโโโโโโโโค
โSum โ78.00โ 2327.00โ
โฐโโโโโโโโโโดโโโโโโดโโโโโโโโโฏVerify Excel
You may compare the result, with our previous calculation with Excel.
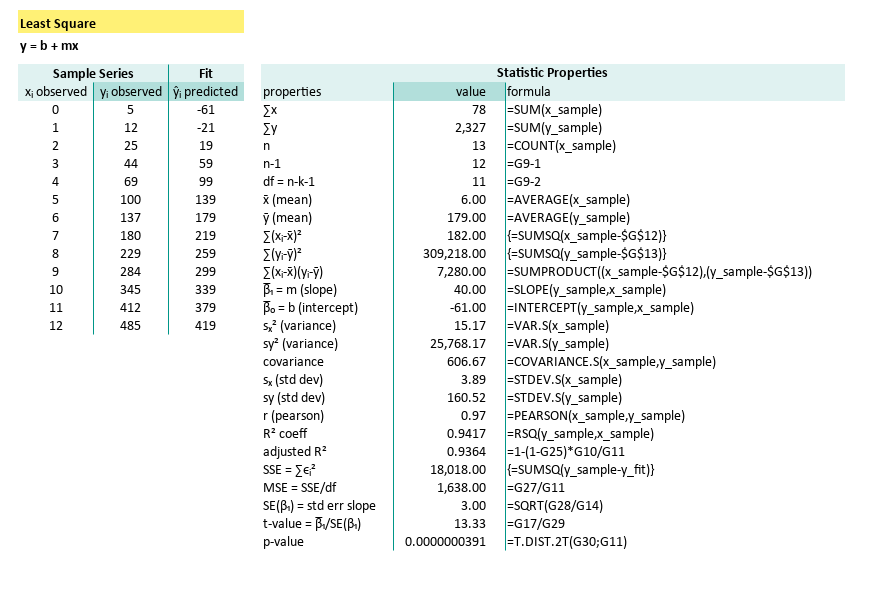
Verify Python
You may compare the result, with our previous calculation with Python.
x (max, min, range) = ( 0.00, 12.00, 12.00 )
y (max, min, range) = ( 5.00, 485.00, 480.00 )
x median = 6.00
y median = 137.00
x mode = 0.00
y mode = 5.00
x kurtosis = -1.20
y kurtosis = -0.73
x skewness = 0.00
y skewness = 0.70
x SE kurtosis = 1.19
y SE kurtosis = 1.19
x SE skewness = 0.62
y SE skewness = 0.62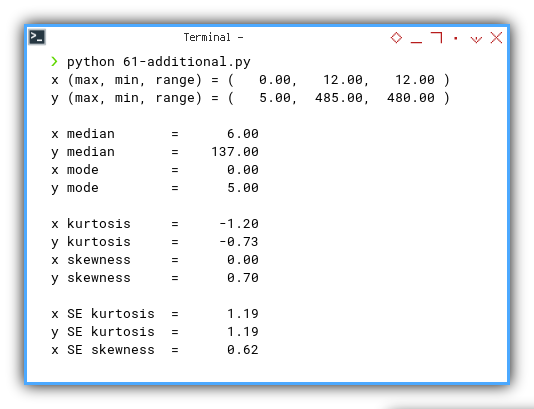
Linear Regression Analysis
You can also analyse linear regression.
PSPPire
Again, fill the necessary dialog. Click OK.
And again, voila, the output viewer.
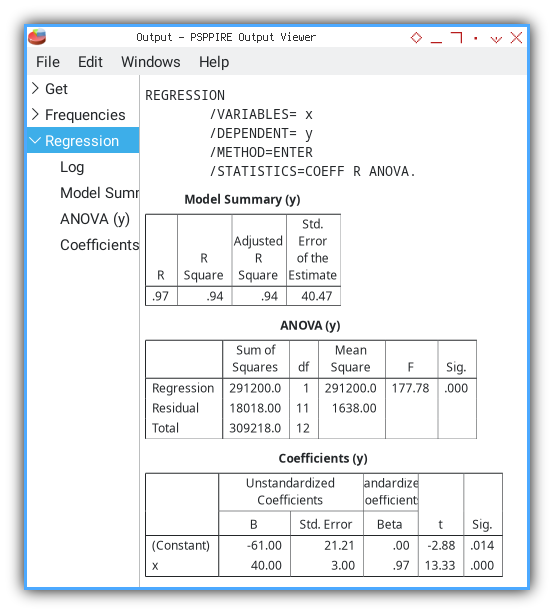
The output is similar following text. The first text is the command line. Followed by tabular data.
REGRESSION
/VARIABLES= x
/DEPENDENT= y
/METHOD=ENTER
/STATISTICS=COEFF R ANOVA.The first is model summary. You can see the table match our previous calculation.
Model Summary (y)
โญโโโโฌโโโโโโโโโฌโโโโโโโโโโโโโโโโโโฌโโโโโโโโโโโโโโโโโโโโโโโโโโโฎ
โ R โR SquareโAdjusted R SquareโStd. Error of the Estimateโ
โโโโโผโโโโโโโโโผโโโโโโโโโโโโโโโโโโผโโโโโโโโโโโโโโโโโโโโโโโโโโโค
โ.97โ .94โ .94โ 40.47โ
โฐโโโโดโโโโโโโโโดโโโโโโโโโโโโโโโโโโดโโโโโโโโโโโโโโโโโโโโโโโโโโโฏThe second is ANOVA. You can see the table match our previous calculation. With additional F-statistics.
ANOVA (y)
โญโโโโโโโโโโโฌโโโโโโโโโโโโโโโฌโโโฌโโโโโโโโโโโโฌโโโโโโโฌโโโโโฎ
โ โSum of SquaresโdfโMean Squareโ F โSig.โ
โโโโโโโโโโโโผโโโโโโโโโโโโโโโผโโโผโโโโโโโโโโโโผโโโโโโโผโโโโโค
โRegressionโ 291200.0โ 1โ 291200.0โ177.78โ.000โ
โResidual โ 18018.00โ11โ 1638.00โ โ โ
โTotal โ 309218.0โ12โ โ โ โ
โฐโโโโโโโโโโโดโโโโโโโโโโโโโโโดโโโดโโโโโโโโโโโโดโโโโโโโดโโโโโฏThe last is Coefficients. This is also match our calculation. Except that we haven’t calculate the standard error of constant yet.
Coefficients (y)
โญโโโโโโโโโโโฌโโโโโโโโโโโโโโโโโโโโโโโโโโโโโฌโโโโโโโโโโโโโโโโโโโโโโโโโโฌโโโโโโฌโโโโโฎ
โ โ Unstandardized CoefficientsโStandardized Coefficientsโ โ โ
โ โโโโโโโโโโโโโโฌโโโโโโโโโโโโโโโโผโโโโโโโโโโโโโโโโโโโโโโโโโโค โ โ
โ โ B โ Std. Error โ Beta โ t โSig.โ
โโโโโโโโโโโโผโโโโโโโโโโโโโผโโโโโโโโโโโโโโโโผโโโโโโโโโโโโโโโโโโโโโโโโโโผโโโโโโผโโโโโค
โ(Constant)โ -61.00โ 21.21โ .00โ-2.88โ.014โ
โx โ 40.00โ 3.00โ .97โ13.33โ.000โ
โฐโโโโโโโโโโโดโโโโโโโโโโโโโดโโโโโโโโโโโโโโโโดโโโโโโโโโโโโโโโโโโโโโโโโโโดโโโโโโดโโโโโฏVerify Excel
You may compare the result, with our previous calculation with excel and python.
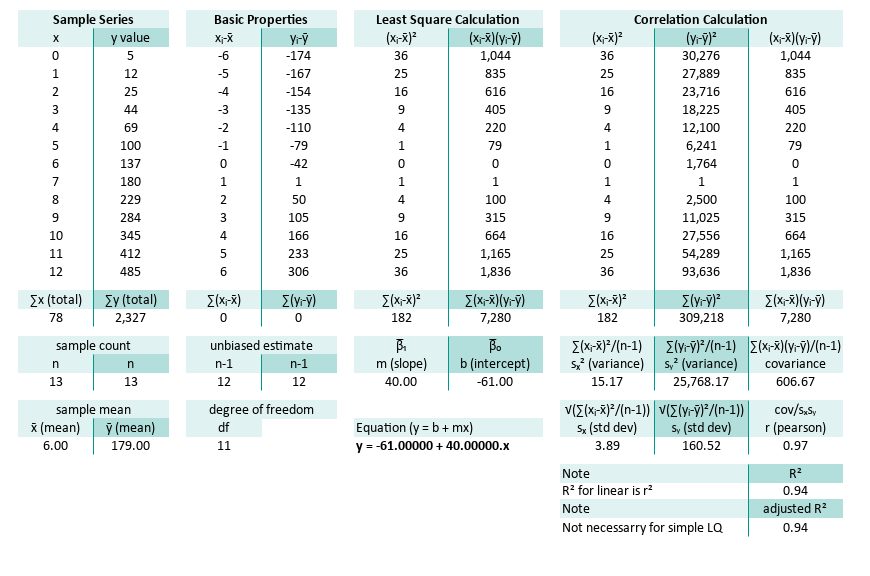
And also the right part of the worksheet.
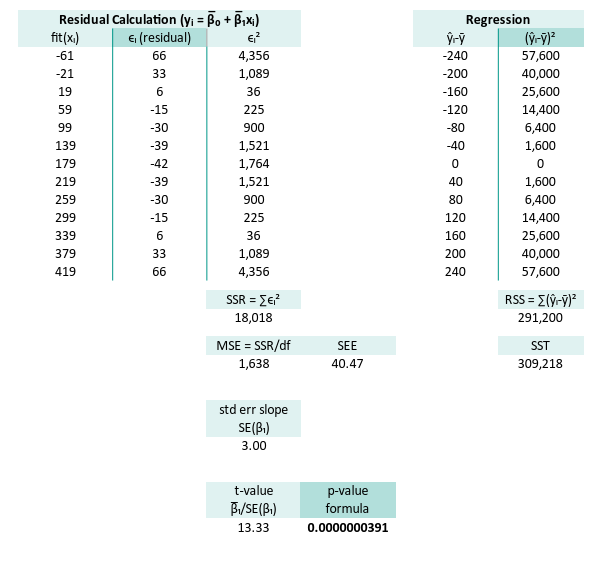
Verify Python
You may compare the result, with our previous calculation with Python.
n = 13
โx (total) = 78.00
โy (total) = 2327.00
xฬ (mean) = 6.00
yฬ (mean) = 179.00
โ(xแตข-xฬ) = 0.00
โ(yแตข-yฬ) = 0.00
โ(xแตข-xฬ)ยฒ = 182.00
โ(yแตข-yฬ)ยฒ = 309218.00
โ(xแตข-xฬ)(yแตข-yฬ) = 7280.00
m (slope) = 40.00
b (intercept) = -61.00
Equation y = -61.00 + 40.00.x
sโยฒ (variance) = 14.00
syยฒ (variance) = 23786.00
covariance = 560.00
sโ (std dev) = 3.74
sy (std dev) = 154.23
r (pearson) = 0.97
Rยฒ = 0.94
SSR = โฯตยฒ = 18018.00
MSE = โฯตยฒ/(n-2) = 1638.00
SE(ฮฒโ) = โ(MSE/sโ) = 3.00
t-value = ฮฒฬ
โ/SE(ฮฒโ) = 13.33
Further Analysis
If you work regularly with statistic, PSPP is your friend. There are a lot that can be done with PSPPire, but this is article is never meant to cover all PSPP feature.
I think that’s all with PSPPire.
What’s the Next Chapter ๐ค?
Beside python there is this R, Julia for statistical analysis. And also Go, so you can integrate with your application seamlessly.
Consider continuing your exploration with [ Trend - Language - R - Part One ].
What’s left behind ๐ค?
We are going to calculate regression for quadratic, cubic, and even spline. After that we are going to calculate correlation between two data series, with the same x-axis. Then correlation of fluctuation of, a data series against other fluctuation.